
【题目】设a为实数,函数![]() ,
,
(1)若![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)是否存在实数a,使得函数![]() 在区间
在区间![]() 上既有最大值又有最小值?若存在,求出实数a的取值范围;若不存在,请说明理由;
上既有最大值又有最小值?若存在,求出实数a的取值范围;若不存在,请说明理由;
(3)写出函数![]() 在R上的零点个数(不必写出过程).
在R上的零点个数(不必写出过程).
【答案】(1)![]() (2)不存在这样的实数
(2)不存在这样的实数![]() ,理由见解析(3)见解析
,理由见解析(3)见解析
【解析】
(1)代入![]() 的值,通过讨论
的值,通过讨论![]() 的范围,求出不等式的解集即可;
的范围,求出不等式的解集即可;
(2)通过讨论![]() 的范围,求出函数的单调区间,再求出函数的最值,得到关于
的范围,求出函数的单调区间,再求出函数的最值,得到关于![]() 的不等式组,解出并判断即可;
的不等式组,解出并判断即可;
(3)通过讨论![]() 的范围,判断函数的零点个数即可
的范围,判断函数的零点个数即可
(1)当![]() 时,
时,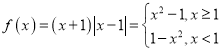 ,
,
则当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() ,故
,故![]() ;
;
当![]() 时,
时,![]() ,解集为
,解集为![]() ,
,
综上,![]() 的解集为
的解集为![]()
(2)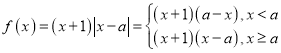 ,显然,
,显然,![]() ,
,
①当![]() 时,则
时,则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因为函数![]() 在
在![]() 上既有最大值又有最小值,
上既有最大值又有最小值,
所以![]() ,
,![]() ,
,
则 ,即
,即![]() ,解得
,解得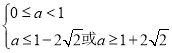 ,
,
故不存在这样的实数![]() ;
;
②当![]() 时,则
时,则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因为函数![]() 在
在![]() 上既有最大值又有最小值,
上既有最大值又有最小值,
故![]() ,
,![]() ,
,
则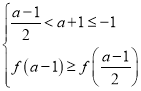 ,即
,即![]() ,解得
,解得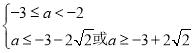 ,
,
故不存在这样的实数![]() ;
;
③当![]() 时,则
时,则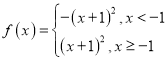 为
为![]() 上的递增函数,
上的递增函数,
故函数![]() 在
在![]() 上不存在最大值和最小值,
上不存在最大值和最小值,
综上,不存在这样的实数![]()
(3)当![]() 或
或![]() 时,函数
时,函数![]() 的零点个数为1;
的零点个数为1;
当![]() 或
或![]() 时,函数
时,函数![]() 的零点个数为2;
的零点个数为2;
当![]() 时,函数
时,函数![]() 的零点个数为3
的零点个数为3


科目:高中数学 来源: 题型:
【题目】(1)求与直线3x+4y-7=0垂直,且与原点的距离为6的直线方程;
(2)求经过直线l1:2x+3y-5=0与l2:7x+15y+1=0的交点,且平行于直线x+2y-3=0的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,外接球的球心为О,点E是侧棱
,外接球的球心为О,点E是侧棱![]() 上的一个动点.有下列判断:
上的一个动点.有下列判断:

①直线AC与直线![]() 是异面直线;
是异面直线;
②![]() 一定不垂直
一定不垂直![]() ;
;
③三棱锥![]() 的体积为定值;
的体积为定值;
④![]() 的最小值为
的最小值为![]()
⑤平面![]() 与平面
与平面![]() 所成角为
所成角为![]()
其中正确的序号为_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某省各景区在大众中的熟知度,随机从本省![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家![]() 级旅游景区?”,统计结果如下表所示:
级旅游景区?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
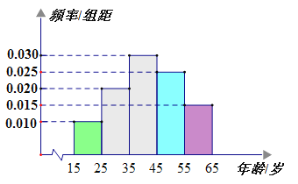
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄段在
人,求所抽取的人中恰好没有年龄段在![]() 的概率
的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:

其中: 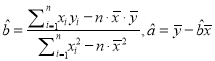 ,
, ![]() ,
, ![]()
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(
;(![]() 的值精确到0.01)
的值精确到0.01)
(3)若规定,一个人的收缩压为标准值的0.9~1.06倍,则为血压正常人群;收缩压为标准值的1.06~1.12倍,则为轻度高血压人群;收缩压为标准值的1.12~1.20倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg的70岁的老人,属于哪类人群?
【答案】(1)答案见解析;(2) ![]() ;(3)中度高血压人群.
;(3)中度高血压人群.
【解析】试题分析:(1)将数据对应描点,即得散点图,(2)先求均值,再代人公式求![]() ,利用
,利用![]() 求
求![]() ,(3)根据回归直线方程求自变量为180时对应函数值,再求与标准值的倍数,确定所属人群.
,(3)根据回归直线方程求自变量为180时对应函数值,再求与标准值的倍数,确定所属人群.
试题解析:(1) 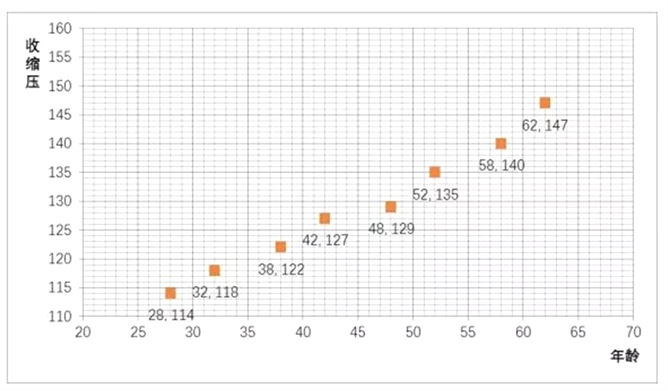
(2)![]()
![]()
∴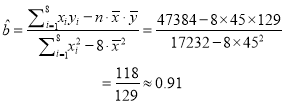
![]()
∴回归直线方程为![]() .
.
(3)根据回归直线方程的预测,年龄为70岁的老人标准收缩压约为![]() (mmHg)∵
(mmHg)∵![]()
∴收缩压为180mmHg的70岁老人为中度高血压人群.
【题型】解答题
【结束】
19
【题目】如图,四棱柱![]() 的底面为菱形,
的底面为菱形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 底面
底面![]() ,且直线
,且直线![]() 与平面
与平面![]() 所成线面角的正弦值为
所成线面角的正弦值为![]() ,求
,求![]() 的长.
的长.
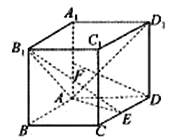
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列![]() 的公比为
的公比为![]() ,其前
,其前![]() 项和为
项和为![]() ,前
,前![]() 项之积为
项之积为![]() ,并且满足条件:
,并且满足条件:![]() ,
,![]() ,
,![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() 是数列
是数列![]() 中的最大值 D. 数列
中的最大值 D. 数列![]() 无最小值
无最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com