
【题目】定义:对于任意![]() ,
,![]() 仍为数列
仍为数列![]() 中的项,则称数列
中的项,则称数列![]() 为“回归数列”.
为“回归数列”.
(1)己知![]() (
(![]() ),判断数列
),判断数列![]() 是否为“回归数列”,并说明理由;
是否为“回归数列”,并说明理由;
(2)若数列![]() 为“回归数列”,
为“回归数列”,![]() ,
,![]() ,且对于任意
,且对于任意![]() ,均有
,均有![]() 成立.①求数列
成立.①求数列![]() 的通项公式;②求所有的正整数s,t,使得等式
的通项公式;②求所有的正整数s,t,使得等式![]() 成立.
成立.
【答案】(1)![]() 不是“回归数列”,说明见解析(2)①
不是“回归数列”,说明见解析(2)①![]() ,②使得等式成立的所有的正整数s,
,②使得等式成立的所有的正整数s,![]() 的值是s=1,t=3
的值是s=1,t=3
【解析】
(1)假设![]() 是“回归数列”,则对任意
是“回归数列”,则对任意![]() ,总存在
,总存在![]() ,使
,使![]() 成立,列出方程即可求解。
成立,列出方程即可求解。
(2)①因为![]() ,所以
,所以![]() ,根据
,根据![]() 为“回归数列”,得
为“回归数列”,得![]() ,可得以数列
,可得以数列![]() 为等差数列,即可求解;
为等差数列,即可求解;
②由![]() ,求得
,求得![]() ,分类讨论,根据数列的单调性,即可求解。
,分类讨论,根据数列的单调性,即可求解。
(1)假设![]() 是“回归数列”
是“回归数列”
则对任意![]() ,总存在
,总存在![]() ,使
,使![]() 成立,
成立,
即![]() ,即
,即![]() ,
,
此时等式左边为奇数.右边为偶数,不成立,所以假设不成立
所以![]() 不是“回归数列”;
不是“回归数列”;
(2)①因为![]() ,所以
,所以![]() ,
,
所以![]() 且
且![]() ,
,
又因为![]() 为“回归数列”,所以
为“回归数列”,所以![]() ,
,
即![]() ,所以数列
,所以数列![]() 为等差数列.
为等差数列.
又因为![]() 所以
所以![]() .
.
②因为![]() ,所以
,所以![]()
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() 式整理为
式整理为![]() ,不成立,
,不成立,
当![]() 时,
时,![]() 式整理为
式整理为![]() ,
,
设![]() ,因为
,因为![]() ,
,
所以![]() 时,
时,![]() 时,
时,![]()
所以![]() ,所以s无解
,所以s无解
当![]() 时,
时,![]() 式整理
式整理![]() ,因为
,因为![]() ,所以s=1
,所以s=1
综合所述,使得等式成立的所有的正整数s,的值是s=1,t=3


科目:高中数学 来源: 题型:
【题目】某外卖企业两位员工今年![]() 月某
月某![]() 天日派送外卖量的数据(单位:件),如茎叶图所示针对这
天日派送外卖量的数据(单位:件),如茎叶图所示针对这![]() 天的数据,下面说法错误的是( )
天的数据,下面说法错误的是( )
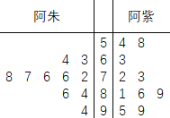
A.阿朱的日派送量的众数为![]() B.阿紫的日派送量的中位数为
B.阿紫的日派送量的中位数为![]()
C.阿朱的日派送量的中位数为![]() D.阿朱的日派送外卖量更稳定
D.阿朱的日派送外卖量更稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于任意![]() ,
,![]() 仍为数列
仍为数列![]() 中的项,则称数列
中的项,则称数列![]() 为“回归数列”.
为“回归数列”.
(1)己知![]() (
(![]() ),判断数列
),判断数列![]() 是否为“回归数列”,并说明理由;
是否为“回归数列”,并说明理由;
(2)若数列![]() 为“回归数列”,
为“回归数列”,![]() ,
,![]() ,且对于任意
,且对于任意![]() ,均有
,均有![]() 成立.①求数列
成立.①求数列![]() 的通项公式;②求所有的正整数s,t,使得等式
的通项公式;②求所有的正整数s,t,使得等式![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
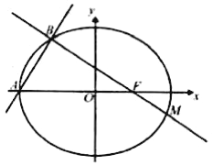
【题目】如图,在平面直角坐标系xOy中,已知焦点在x轴上,离心率为![]() 的椭圆E的左顶点为A,点A到右准线的距离为6.
的椭圆E的左顶点为A,点A到右准线的距离为6.
(1)求椭圆E的标准方程;
(2)过点A且斜率为![]() 的直线与椭圆E交于点B,过点B与右焦点F的直线交椭圆E于M点,求M点的坐标.
的直线与椭圆E交于点B,过点B与右焦点F的直线交椭圆E于M点,求M点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上任意一点到两焦点
上任意一点到两焦点![]() 距离之和为
距离之和为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与椭圆C交于
与椭圆C交于![]() 两点.点
两点.点![]() 为椭圆上一点,求
为椭圆上一点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人各有三张卡片,甲的卡片分别标有数字1、2、3,乙的卡片分别标有数字0、1、3.两人各自随机抽出一张,甲抽出的卡片上的数字记为![]() ,乙抽出的卡片上的数字记为
,乙抽出的卡片上的数字记为![]() ,则
,则![]() 与
与![]() 的积为奇数的概率为________.
的积为奇数的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行篮球决赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,决赛结束). 根据前期比赛成绩,甲队的主客场安排依次为“主主客客主”. 设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以3:1获胜的概率为( )
A.0.15B.0.21C.0.24D.0.30
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
未发病 | 发病 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能够有多大把握认为疫苗有效?
(参考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com