
【题目】如图,在平行六面体ABCD﹣A1B1C1D1中,AA1=A1D,AB=BC,∠ABC=120°.
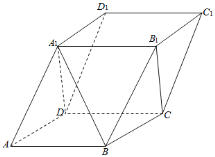
(1)证明:AD⊥BA1;
(2)若平面ADD1A1⊥平面ABCD,且A1D=AB,求直线BA1与平面A1B1CD所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)取AD中点O,连接OB,OA1,BD,推导出AD⊥OA1,△ABD是等边三角形,从而AD⊥OB,进而AD⊥平面A1OB,由此能证明AD⊥BA1.
(2)推导出OA、OA1、OB两两垂直,以O为坐标原点,分别以OA、OB、OA1所在射线为x、y、z轴建立空间直角坐标系Oxyz,利用向量法能求出直线BA1与平面A1B1CD所成角的正弦值.
证明:(1)取AD中点O,连接OB,OA1,BD,
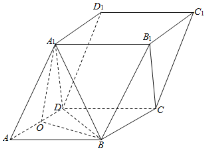
∵AA1=A1D,∴AD⊥OA1,
又∠ABC=120°,AD=AB,∴△ABD是等边三角形,
∴AD⊥OB,∴AD⊥平面A1OB,
∵A1B平面A1OB,∴AD⊥A1B.
(2)∵平面ADD1A1⊥平面ABCD,
平面ADD1A1∩平面ABCD=AD,
又A1O⊥AD,∴A1O⊥平面ABCD,∴OA、OA1、OB两两垂直,
以O为坐标原点,分别以OA、OB、OA1所在射线为x、y、z轴建立如图空间直角坐标系O﹣xyz,

设AB=AD=A1D=2,则A(1,0,0),![]() ,
,![]() ,D(﹣1,0,0),.
,D(﹣1,0,0),.
则![]() ,
,![]() ,
,![]() ,
,
设平面A1B1CD的法向量![]()
则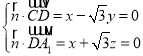 ,令
,令![]() ,则y=1,z=﹣1,可取
,则y=1,z=﹣1,可取![]() ,
,
设直线BA1与平面A1B1CD所成角为θ,
则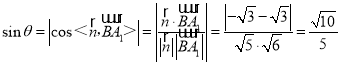 .
.
∴直线BA1与平面A1B1CD所成角的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,下表是2013-2017年全国快递业务量(x亿件:精确到0.1)及其增长速度(y%)的数据
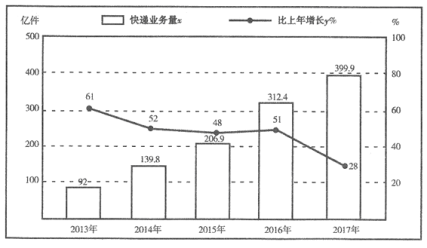
(1)试计算2012年的快递业务量;
(2)分别将2013年,2014年,…,2017年记成年的序号t:1,2,3,4,5;现已知y与t具有线性相关关系,试建立y关于t的回归直线方程![]() ;
;
(3)根据(2)问中所建立的回归直线方程,估算2019年的快递业务量
附:回归直线的斜率和截距地最小二乘法估计公式分别为: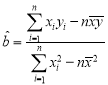 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
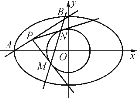
【题目】已知椭圆C:![]() =1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=![]() (c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(1)若椭圆C经过两点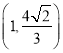 、
、 ,求椭圆C的方程;
,求椭圆C的方程;
(2)当c为定值时,求证:直线MN经过一定点E,并求![]() ·
·![]() 的值(O是坐标原点);
的值(O是坐标原点);
(3)若存在点P使得△PMN为正三角形,试求椭圆离心率的取值范围..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]()
(l)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 设
设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧棱
是矩形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() .
.
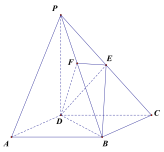
(1)证明:![]() 平面
平面![]() ;
;
(2)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() ,求
,求![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道![]() 和唯众传媒联合制作的
和唯众传媒联合制作的![]() 开讲啦
开讲啦![]() 是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区的100名观众,得到如表的
是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区的100名观众,得到如表的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是B地区当中“非常满意”的观众的概率为
列联表,已知在被调查的100名观众中随机抽取1名,该观众是B地区当中“非常满意”的观众的概率为![]() .
.
非常满意 | 满意 | 合计 | |
A | 30 | 15 | |
B | |||
合计 |
![]() 完成上述表格并根据表格判断是否有
完成上述表格并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系;
的把握认为观众的满意程度与所在地区有关系;
![]() 若以抽样调查的频率为概率,从A地区随机抽取3人,设抽到的观众“非常满意”的人数为X,求X的分布列和期望.
若以抽样调查的频率为概率,从A地区随机抽取3人,设抽到的观众“非常满意”的人数为X,求X的分布列和期望.
|
|
|
|
|
|
|
|
附:参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆E :![]() 的焦距为4,两条准线间的距离为8,A,B分别为椭圆E的左、右顶点.
的焦距为4,两条准线间的距离为8,A,B分别为椭圆E的左、右顶点.

(1)求椭圆E 的标准方程;
(2)已知图中四边形ABCD 是矩形,且BC=4,点M,N分别在边BC,CD上,AM与BN相交于第一象限内的点P .①若M,N分别是BC,CD的中点,证明:点P在椭圆E上;②若点P在椭圆E上,证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1—ABCE,其中平面D1AE⊥平面ABCE.
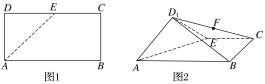
(1)证明:BE⊥平面D1AE;
(2)设F为CD1的中点,在线段AB上是否存在一点M,使得MF∥平面D1AE,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() 两顶点
两顶点![]() ,短轴长为4,焦距为2,过点
,短轴长为4,焦距为2,过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点.设直线
两点.设直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
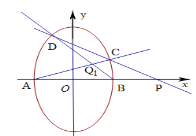
(1)求椭圆的方程;
(2)求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
(3)求证:点![]() 的横坐标为定值.
的横坐标为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com