
【题目】(1)数列{an}的前n项和为Sn=10n﹣n2,求数列{|an|}的前n项和.
(2)已知等差数列{an}满足a2=0,a6+a8=﹣10.求数列{![]() }的前n项和.
}的前n项和.
【答案】(1)Tn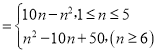 ;(2)Hn
;(2)Hn![]() .
.
【解析】
(1)根据Sn=10n﹣n2,利用通项与前n项和的关系,n≥2时,an=Sn﹣Sn﹣1,(n=1时也成立)求得an.令an≥0,解得n≤5.可得n≤5时,{|an|}的前n项和Tn=a1+a2+……+an=Sn.n≥6时,{|an|}的前n项和Tn=a1+a2+……a5﹣a6+……﹣an=2S5﹣Sn.即可得出Tn.
(2)设等差数列{an}的公差为d,由a2=0,a6+a8=﹣10.可得a1+d=0,2a1+12d=﹣10,联立解得:a1,d,可得an.于是![]() .利用错位相减法即可得出.
.利用错位相减法即可得出.
(1)∵Sn=10n﹣n2,
∴n≥2时,an=Sn﹣Sn﹣1=10n﹣n2﹣[10(n﹣1)﹣(n﹣1)2]=11﹣2n,
当n=1时,![]() 满足上式,故an=11﹣2n.
满足上式,故an=11﹣2n.
令an≥0,解得n≤5.
∴n≤5时,{|an|}的前n项和Tn=a1+a2+……+an=Sn=10n﹣n2.
n≥6时,{|an|}的前n项和Tn=a1+a2+……a5﹣a6+……﹣an=2S5﹣Sn=2×(50﹣25)﹣(10n﹣n2)=n2﹣10n+50.
综上可得:Tn .
.
(2)设等差数列{an}的公差为d,∵a2=0,a6+a8=﹣10.
∴a1+d=0,2a1+12d=﹣10,
联立解得:a1=1,d=﹣1,
∴an=1﹣(n﹣1)=2﹣n.
∴![]() .
.
∴数列{![]() }的前n项和Hn=1+0
}的前n项和Hn=1+0![]() .
.
![]() Hn
Hn![]() 0
0![]() .
.
相减可得:![]() Hn=
Hn=![]() ,
,
![]() ,
,
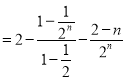
![]() .
.
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数据![]() 是宜昌市
是宜昌市![]() 个普通职工的年收入,设这
个普通职工的年收入,设这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A. 年收入平均数可能不变,中位数可能不变,方差可能不变
B. 年收入平均数大大增大,中位数可能不变,方差变大
C. 年收入平均数大大增大,中位数可能不变,方差也不变
D. 年收入平均数大大增大,中位数一定变大,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在极坐标系下,已知圆O:![]() 和直线
和直线![]()
(1)求圆O和直线l的直角坐标方程;
(2)当![]() 时,求直线l与圆O公共点的一个极坐标.
时,求直线l与圆O公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①设某大学的女生体重![]() 与身高
与身高![]() 具有线性相关关系,根据一组样本数据
具有线性相关关系,根据一组样本数据![]() ,用最小二乘法建立的线性回归方程为
,用最小二乘法建立的线性回归方程为![]() ,则若该大学某女生身高增加
,则若该大学某女生身高增加![]() ,则其体重约增加
,则其体重约增加![]() ;
;
②关于![]() 的方程
的方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③过定圆![]() 上一定点
上一定点![]() 作圆的动弦
作圆的动弦![]() ,
,![]() 为原点,若
为原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
④已知![]() 是椭圆
是椭圆![]() 的左焦点,设动点
的左焦点,设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() ,则直线
,则直线![]() (
(![]() 为原点)的斜率的取值范围是
为原点)的斜率的取值范围是![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为 ( )
①我离开学校不久,发现自己把作业本忘在教室,于是立刻返回教室里取了作业本再回家;
②我放学回家骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;

③我放学从学校出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
A.(1)(2)(4)B.(4)(1)(2)C.(4)(1)(3)D.(4)(2)(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com