
【题目】某植物学家培养出一种观赏性植物,会开出红花或黄花,已知该植物第一代开红花和黄花的概率都是![]() ,从第二代开始,若上一代开红花,则这一代开红花的概率是
,从第二代开始,若上一代开红花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() ;若上一代开黄花,则这一代开红花的概率是
;若上一代开黄花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() .记第n代开红花的概率为
.记第n代开红花的概率为![]() ,第n代开黄花的概率为
,第n代开黄花的概率为![]() .
.
(1)求![]() ;
;
(2)①证明:数列![]() 为等比数列;
为等比数列;
②第![]() 代开哪种颜色花的概率更大?
代开哪种颜色花的概率更大?
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为菱形,
的底面为菱形,![]() ,
,![]() .平面
.平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() //平面
//平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
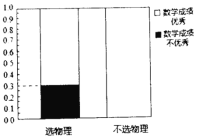
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附:
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为平行四边形,
为平行四边形,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上(不含端点)是否存在一点
上(不含端点)是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治理空气污染,某市设![]() 个监测站用于监测空气质量指数
个监测站用于监测空气质量指数![]() ,其中在轻度污染区、中度污染区、重度污染区分别设有
,其中在轻度污染区、中度污染区、重度污染区分别设有![]() 、
、![]() 、
、![]() 个监测站,并以
个监测站,并以![]() 个监测站测得的
个监测站测得的![]() 的平均值为依据播报该市的空气质量.
的平均值为依据播报该市的空气质量.
(1)若某日播报的![]() 为
为![]() ,已知轻度污染区
,已知轻度污染区![]() 平均值为
平均值为![]() ,中度污染区
,中度污染区![]() 平均值为
平均值为![]() ,求重试污染区
,求重试污染区![]() 平均值;
平均值;
(2)如图是![]() 年
年![]() 月份
月份![]() 天的
天的![]() 的频率分布直方图,
的频率分布直方图,![]() 月份仅有
月份仅有![]() 天
天![]() 在
在![]() 内.
内.

①某校参照官方公布的![]() ,如果周日
,如果周日![]() 小于
小于![]() 就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
②环卫部门从![]() 月份
月份![]() 不小于
不小于![]() 的数据中抽取两天的数据进行研究,求抽取的这两天中
的数据中抽取两天的数据进行研究,求抽取的这两天中![]() 值都在
值都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com