设函数f(x)=-x(x-a)2(x∈R),其中a∈R.
(Ⅰ)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)当a≠0时,求函数f(x)的极大值和极小值;
(Ⅲ)当a>3时,证明存在k∈[-1,0],使得不等式f(k-cosx)≥f(k2-cos2x)对任意的x∈R恒成立.
分析:(Ⅰ)求出f(2)和f′(2),利用点斜式写切线方程.
(Ⅱ)求导,令f′(x)=0,再考虑f(x)的单调性,求极值即可.
(Ⅲ)有(Ⅱ)可知当a>3时f(x)为单调函数,利用单调性直接转化为k-cosx≤k2-cos2x恒成立,分离参数求解即可.
解答:解:(Ⅰ)解:当a=1时,f(x)=-x(x-1)
2=-x
3+2x
2-x,得f(2)=-2,且f'(x)=-3x
2+4x-1,f'(2)=-5.
所以,曲线y=-x(x-1)
2在点(2,-2)处的切线方程是y+2=-5(x-2),整理得5x+y-8=0.
(Ⅱ)解:f(x)=-x(x-a)
2=-x
3+2ax
2-a
2xf'(x)=-3x
2+4ax-a
2=-(3x-a)(x-a).
令f'(x)=0,解得
x=或x=a.
由于a≠0,以下分两种情况讨论.
(1)若a>0,当x变化时,f'(x)的正负如下表:
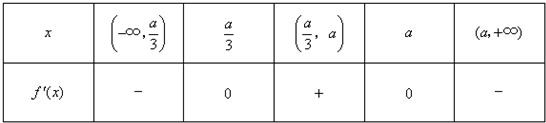
因此,函数f(x)在
x=处取得极小值
f(),且
f()=-a3;
函数f(x)在x=a处取得极大值f(a),且f(a)=0.
(2)若a<0,当x变化时,f'(x)的正负如下表:

因此,函数f(x)在x=a处取得极小值f(a),且f(a)=0;
函数f(x)在
x=处取得极大值
f(),且
f()=-a3.
(Ⅲ)证明:由a>3,得
>1,当k∈[-1,0]时,k-cosx≤1,k
2-cos
2x≤1.
由(Ⅱ)知,f(x)在(-∞,1]上是减函数,要使f(k-cosx)≥f(k
2-cos
2x),x∈R
只要k-cosx≤k
2-cos
2x(x∈R)
即cos
2x-cosx≤k
2-k(x∈R)①
设
g(x)=cos2x-cosx=(cosx-)2-,则函数g(x)在R上的最大值为2.
要使①式恒成立,必须k
2-k≥2,即k≥2或k≤-1.
所以,在区间[-1,0]上存在k=-1,使得f(k-cosx)≥f(k
2-cos
2x)对任意的x∈R恒成立.
点评:本小题主要考查运用导数研究函数的性质、曲线的切线方程,函数的极值、解不等式等基础知识,考查综合分析和解决问题的能力及分类讨论的思想方法.




