
分析 (1)根据函数的奇偶性得到f(0)=0,求出a的值即可;令-x>0,得到x<0,根据函数的奇偶性求出函数的解析式即可;
(2)根据函数解析式,建立方程,即可得出结论.
解答 解:(1)∵f(x)为定义在R上的奇函数,
∴f(0)=a=0,
由题意x≥0时:f(x)=x2-4x,
设x<0,则-x>0,
则f(-x)=x2+4x=-f(x),
故x<0时,f(x)=-x2-4x,
故f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x,x≥0}\\{-{x}^{2}-4x,x<0}\end{array}\right.$.
(2)当x≥0时,x2-4x=x+6,可得x=6;
x<0时,f(x)=-x2-4x=x+6,可得x=-2或-3.
综上所述,方程的解为6,-2或-3.
点评 本题考查了函数的奇偶性问题,考查求函数的解析式,是一道基础题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | -5 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{2π}{9}$个单位 | B. | 向左平移$\frac{2π}{9}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向左平移$\frac{2π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
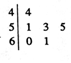 为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )
为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )| A. | 52 | B. | 53 | C. | 54 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x,g(x)=${(\sqrt{x}\;)^2}$ | B. | f(x)=x+1,g(x)=$\frac{{{x^2}-1}}{x-1}$ | ||
| C. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=log22x,g(x)=2log2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com