
【题目】已知函数f(x)=(sinx+cosx)2+cos2x
(1)求f(x)最小正周期;
(2)求f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
【答案】
(1)解:∵函数f(x)=(sinx+cosx)2+cos2x=1+sin2x+cos2x=1+ ![]() sin(2x+
sin(2x+ ![]() ),
),
∴它的最小正周期为 ![]() =π
=π
(2)解:在区间[ ![]() ]上,2x+
]上,2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],故当2x+
],故当2x+ ![]() =
= ![]() 时,f(x)取得最小值为 1+
时,f(x)取得最小值为 1+ ![]() ×(﹣
×(﹣ ![]() )=0,
)=0,
当2x+ ![]() =
= ![]() 时,f(x)取得最大值为 1+
时,f(x)取得最大值为 1+ ![]() ×1=1+
×1=1+ ![]()
【解析】(1)由条件利用三角恒等变换求得f(x)的解析式,再利用正弦函数的周期性求得f(x)最小正周期.(2)由条件利用正弦函数的定义域和值域,求得f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
【考点精析】掌握三角函数的最值是解答本题的根本,需要知道函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD. 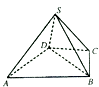
(Ⅰ)求证:SB=SD;
(Ⅱ)若∠BCD=120°,M为棱SA的中点,求证:DM∥平面SBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0),f(2)=0,且方程f(x)=x有等根.
(1)求f(x)的解析式
(2)是否存在常数m,n(m<n),使f(x)的定义域和值域分别是[m,n]和[2m,2n]?如存在,求出m,n的值;如不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l交椭圆4x2+5y2=80于M、N两点,椭圆的上顶点为B点,若△BMN的重心恰好落在椭圆的右焦点上,则直线l的方程是( )
A.5x+6y﹣28=0
B.5x﹣6y﹣28=0
C.6x+5y﹣28=0
D.6x﹣5y﹣28=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,一动圆经过点
中,一动圆经过点![]() 且与直线
且与直线![]() 相切,设该动圆圆心的轨迹方程为曲线
相切,设该动圆圆心的轨迹方程为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() 的内切圆的方程为
的内切圆的方程为![]() ,将
,将![]() 表示成
表示成![]() 的函数,并求
的函数,并求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com