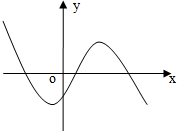考点:函数的图象
专题:函数的性质及应用,导数的概念及应用
分析:由已知中函数f(x)=ax3+bx2+cx+d的图象,根据其与y轴交点的位置,可以判断d的符号,进而根据其单调性和极值点的位置,可以判断出其中导函数图象的开口方向(可判断a的符号)及对应函数两个根的情况,结合韦达定理,可分析出b,c的符号,进而得到答案.
解答:
解:∵函数f(x)=ax3+bx2+cx+d的图象与y轴交点的纵坐标为负,故d<0;
∵f(x)=ax3+bx2+cx+d的图象有两个递减区间,有两个递增区间,
∴f′(x)=3ax2+2bx+c的图象开口方向朝下,且于x轴有两个交点,故a<0,
又∵f(x)=ax3+bx2+cx+d的图象的极小值点和极大值点在y轴两侧,且极小点离y轴近,
∴f′(x)=3ax2+2bx+c=0的两根x1,x2满足,
x1+x2>0,则b>0,x1•x2<0,则c>0,
综上a<0,b>0,c>0,d<0,
故选A
点评:本题考查的知识点是函数的图象与图象变化,其中根据图象的形状分析其导函数的性质是解答本题的关键,同时由于本题涉及到导数,二次函数的图象和性质,函数的单调性,函数取极值的条件等诸多难点,故难度比较大.