
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其右顶点为
,其右顶点为![]() ,下顶点为
,下顶点为![]() ,定点
,定点![]() ,
,![]() 的面积为
的面积为![]() ,过点
,过点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点.
两点.
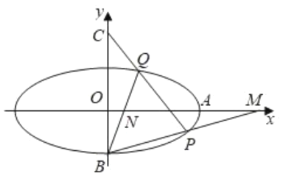
(1)求椭圆![]() 的方程;
的方程;
(2)试探究![]() 的横坐标的乘积是否为定值,若是,请求出该定值;若不是,请说明理由.
的横坐标的乘积是否为定值,若是,请求出该定值;若不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本4元,且以9元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂.根据以往100天的资料统计,得到如表需求量表:
需求量/个 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
天数 | 15 | 25 | 30 | 20 | 10 |
该蛋糕店一天制作了这款蛋糕X(X∈N)个,以x(单位:个,100≤x≤150,x∈N)表示当天的市场需求量,T(单位:元)表示当天出售这款蛋糕获得的利润.
(1)当x=135时,若X=130时获得的利润为T1,X=140时获得的利润为T2,试比较T1和T2的大小;
(2)当X=130时,根据上表,从利润T不少于560元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润T关于市场需求量x的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为ξ,求随机变量ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
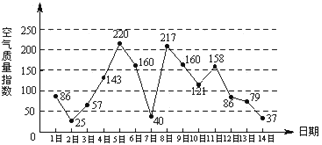
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明在某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前54单没有奖励,超过54单的部分每单奖励20元.
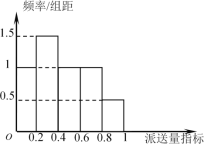
(1)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在![]() 时,日平均派送量为
时,日平均派送量为![]() 单.若将频率视为概率,回答下列问题:
单.若将频率视为概率,回答下列问题:
①估计这100天中的派送量指标的平均数(同一组中的数据用该组区间的中点值作代表) ;
②根据以上数据,设每名派送员的日薪为![]() (单位:元),试分别求出甲、乙两种方案的日薪
(单位:元),试分别求出甲、乙两种方案的日薪![]() 的分布列及数学期望. 请利用数学期望帮助小明分析他选择哪种薪酬方案比较合适?并说明你的理由.
的分布列及数学期望. 请利用数学期望帮助小明分析他选择哪种薪酬方案比较合适?并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从秦朝统一全国币制到清朝末年,圆形方孔铜钱(简称“孔方兄”)是我国使用时间长达两千多年的货币.如图1,这是一枚清朝同治年间的铜钱,其边框是由大小不等的两同心圆围成的,内嵌正方形孔的中心与同心圆圆心重合,正方形外部,圆框内部刻有四个字“同治重宝”.某模具厂计划仿制这样的铜钱作为纪念品,其小圆内部图纸设计如图2所示,小圆直径1厘米,内嵌一个大正方形孔,四周是四个全等的小正方形(边长比孔的边长小),每个正方形有两个顶点在圆周上,另两个顶点在孔边上,四个小正方形内用于刻铜钱上的字.设![]() ,五个正方形的面积和为S.
,五个正方形的面积和为S.

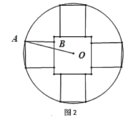
(1)求面积S关于![]() 的函数表达式,并求定义域;
的函数表达式,并求定义域;
(2)求面积S的最小值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市《城市总体规划(![]() 年)》提出到2035年实现“15分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身4个方面构建“15分钟社区生活圈“指标体系,并依据“15分钟社区生活圈”指数高低将小区划分为:优质小区(指数为
年)》提出到2035年实现“15分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身4个方面构建“15分钟社区生活圈“指标体系,并依据“15分钟社区生活圈”指数高低将小区划分为:优质小区(指数为![]() 、良好小区(指数为0.4-0.63、中等小区(指数为0.2~0.4)以及待改进小区(指数为0-0.2)4个等级.下面是三个小区4个方面指标值的调查数据:
、良好小区(指数为0.4-0.63、中等小区(指数为0.2~0.4)以及待改进小区(指数为0-0.2)4个等级.下面是三个小区4个方面指标值的调查数据:
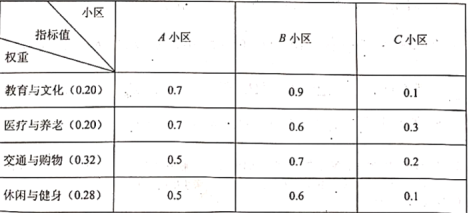
注:每个小区”15分钟社区生活圈”指数![]() 其中
其中![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的权重,
为该小区四个方面的权重,![]() 为该小区四个方面的指标值(小区每一个方面的指标值为
为该小区四个方面的指标值(小区每一个方面的指标值为![]() 之间的一个数值)
之间的一个数值)
现有100个小区的“15分钟社区生活圈“指数数据,整理得到如下频数分布表:

(1)分别判断A、B、C三个小区是否是优质小区,并说明理由;
(2)对这100个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取10个小区进行调查,若在抽取的10个小区中再随机地选取2个小区做深入调查,记这2个小区中为优质小区的个数为ζ,求ζ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】万众瞩目的第14届全国冬季运动运会(简称“十四冬”)于2020年2月16日在呼伦贝尔市盛大开幕,期间正值我市学校放寒假,寒假结束后,某校工会对全校100名教职工在“十四冬”期间每天收看比赛转播的时间作了一次调查,得到如图频数分布直方图:
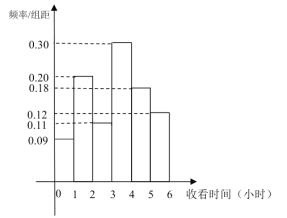
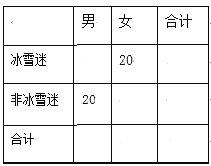
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“冰雪迷”,否则定义为“非冰雪迷”,请根据频率分布直方图补全![]() 列联表;并判断能否有
列联表;并判断能否有![]() 的把握认为该校教职工是否为“冰雪迷”与“性别”有关;
的把握认为该校教职工是否为“冰雪迷”与“性别”有关;
(2)在全校“冰雪迷”中按性别分层抽样抽取6名,再从这6名“冰雪迷”中选取2名作冰雪运动知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
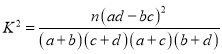 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com