练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知四棱锥的五个顶点都在球O的球面上，，，，是等边三角形，若四棱锥体积的最大值，则球O的表面积为（ ）

    A.B.C.D.

    【答案】C

    【解析】

    画出几何体的图形，判断几何体的体积的最大值的情况，转化求解外接球的半径，然后求解外接球的表面积．

    由题意知，当四棱锥体积最大时，平面平面ABCD，

    设的边长为a，在等腰梯形ABCD中，

    易知，又，可得，

    所以等腰梯形ABCD的面积，

    平面平面ABCD时，棱锥的高即为的高为，

    所以四棱锥体积最大值为，

    解得，

    取BC的中点，因为与是直角三角形，

    所以梯形ABCD的外接圆圆心是边BC的中点；

    又是等边三角形，其外接圆圆心是等边的中心.

    分别过，作梯形ABCD、所在平面的垂线，

    则两垂线的交点O即是四棱锥的外接球球心，

    则四棱锥外接球的半径为：

    ，

    所以球O的表面积为.

    故选：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，点是椭圆上的点.

    （1）求椭圆的标准方程；

    （2）已知斜率存在又不经过原点的直线与圆相切，且与椭圆交于两点.探究：在椭圆上是否存在点，使得，若存在，请求出实数的取值范围，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中石化集团通过与安哥拉国家石油公司合作，获得了安哥拉深海油田区块的开采权，集团在某些区块随机初步勘探了部分旧井，取得了地质资料.进入全面勘探时期后集团按网络点来布置井位来进行全面勘探.由于勘探一口井的费用很高，如果新设计的井位与原有井位重合或接近，便利用旧井的地质资料，不必打这口新井，以节约勘探费用.勘探初期数据资料见下表：

    井位

    1

    2

    3

    4

    5

    6

    坐标

    钻探深度

    2

    4

    5

    6

    8

    10

    出油量

    40

    70

    110

    90

    160

    205

    （1）若16号旧井位置满足线性分布，借助前5组数据所求得的回归直线方程为，且，求，并估计的预报值；

    （2）现准备勘探新井7（1，25），若通过，1，3，5，7号井计算出的，的值与（1）中，的值的差不超过10%，则使用位置最接近的旧井，否则在新位置打井，请判断可否使用旧井？（注：其中的计算结果用四舍五入法保留一位小数）

    参考数据：

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有甲乙丙丁四个人相互之间传球，从甲开始传球，甲等可能地把球传给乙丙丁中的任何一个人，依此类推.

    （1）通过三次传球后，球经过乙的次数为ξ，求ξ的分布列和期望；

    （2）设经过n次传球后，球落在甲手上的概率为an，

    （i）求a1,a2,an；

    （ii）探究：随着传球的次数足够多，球落在甲乙丙丁每个人手上的概率是否相等，并简单说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数=lnx+ax2+(2a+1)x．

    （1）讨论的单调性；

    （2）当a﹤0时，证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，且， ，则数列中的为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在上是减函数，求实数的取值范围；

    （2）若函数在上存在两个极值点，，且，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，圆O是一半径为10米的圆形草坪，为了满足周边市民跳广场舞的需要，现规划在草坪上建一个广场，广场形状如图中虚线部分所示的曲边四边形，其中A，B两点在⊙O上，A，B，C，D恰是一个正方形的四个顶点.根据规划要求，在A，B，C，D四点处安装四盏照明设备，从圆心O点出发，在地下铺设4条到A，B，C，D四点线路OA，OB，OC，OD.

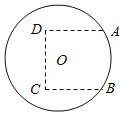
    （1）若正方形边长为10米，求广场的面积；

    （2）求铺设的4条线路OA，OB，OC，OD总长度的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线C：（a＞0，b＞0）的左、右焦点分别为F1，F2，P为双曲线C上的一点，线段PF1与y轴的交点M恰好是线段PF1的中点，，其中O为坐标原点，则双曲线C的渐近线的斜率与离心率分别是( )

    A. ±1， B. 1， C. ±2， D. 2，

    查看答案和解析>>

    同步练习册答案