
分析 分别根据柯西不等式,即可求出,注意等号成立的条件.
解答 解:(1)由柯西不等式($\frac{1}{x}+\frac{1}{y-x}+\frac{1}{3-y}$)[x+(y-x)+(3-y)]≥9,
即$\frac{1}{x}+\frac{1}{y-x}+\frac{1}{3-y}≥3$,
∴当x=1,y=2时,$\frac{1}{x}+\frac{1}{y-x}+\frac{1}{3-y}$的最小值是3;
(2)由柯西不等式$\frac{1}{x^2}+\frac{1}{{{{(y-x)}^2}}}+\frac{1}{{{{(a-y)}^2}}}≥\frac{1}{3}$${(\frac{1}{x}+\frac{1}{y-x}+\frac{1}{a-y})^2}$,
∵$(\frac{1}{x}+\frac{1}{y-x}+\frac{1}{a-y})(x+y-x+a-y)≥9$,
∴$\frac{1}{x}+\frac{1}{y-x}+\frac{1}{a-y}≥\frac{9}{a}$,
∴$\frac{1}{x^2}+\frac{1}{{{{(y-x)}^2}}}+\frac{1}{{{{(a-y)}^2}}}$的最小值是$\frac{27}{a^2}$,
(当$x=\frac{a}{3},y=\frac{2a}{3}$时取到最小值)由题意$\frac{27}{a^2}≥9$,$a≤\sqrt{3}$,
a的最大值是$\sqrt{3}$.
点评 本题考查了柯西不等式,灵活变形是关键,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
 在棱长为1的正方体ABCD-A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$.
在棱长为1的正方体ABCD-A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
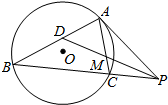 如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )
如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 5$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com