
【题目】已知函数f(x)在R上是增函数,则下列说法正确的是( )
A.y=-f(x)在R上是减函数
B.y=![]() 在R上是减函数
在R上是减函数
C.y=[f(x)]2在R上是增函数
D.y=af(x)(a为实数)在R上是增函数
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2018年10月24日,世界上最长的跨海大桥一港珠澳大桥正式通车![]() 在一般情况下,大桥上的车流速度
在一般情况下,大桥上的车流速度![]() 单位:千米
单位:千米![]() 时
时![]() 是车流密度
是车流密度![]() 单位:辆
单位:辆![]() 千米
千米![]() 的函数
的函数![]() 当桥上的车流密度达到220辆
当桥上的车流密度达到220辆![]() 千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆
千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆![]() 千米时,车流速度为100千米
千米时,车流速度为100千米![]() 时,研究表明:当
时,研究表明:当![]() 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
![]() Ⅱ
Ⅱ![]() 当车流密度x为多大时,车流量
当车流密度x为多大时,车流量![]() 单位时间内通过桥上某观测点的车辆数,单位:辆
单位时间内通过桥上某观测点的车辆数,单位:辆![]() 时
时![]() 可以达到最大?并求出最大值.
可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为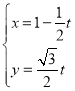 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() 的直角坐标为
的直角坐标为![]() ,曲线
,曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (常数
(常数![]() )满足
)满足![]() .
.
(1)求![]() 的值,并对常数
的值,并对常数![]() 的不同取值讨论函数
的不同取值讨论函数![]() 奇偶性;
奇偶性;
(2)若![]() 在区间
在区间![]() 上单调递减,求
上单调递减,求![]() 的最小值.
的最小值.
(3)若方程![]() 在
在![]() 有解,求
有解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 为椭圆
为椭圆![]() 上不同于点
上不同于点![]() 的点,直线
的点,直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).
(Ⅰ)应收集多少户山区家庭的样本数据?
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有![]() 的把握认为“该地区2017年家庭年收入与地区有关”?
的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动更多人阅读,联合国教科文组织确定每年的![]() 月
月![]() 日为“世界读书日”.设立目的是希望居住在世界各地的人,无论你是年老还是年轻,无论你是贫穷还是富裕,都能享受阅读的乐趣,都能尊重和感谢为人类文明做出过巨大贡献的思想大师们,都能保护知识产权.为了解不同年龄段居民的主要阅读方式,某校兴趣小组在全市随机调查了
日为“世界读书日”.设立目的是希望居住在世界各地的人,无论你是年老还是年轻,无论你是贫穷还是富裕,都能享受阅读的乐趣,都能尊重和感谢为人类文明做出过巨大贡献的思想大师们,都能保护知识产权.为了解不同年龄段居民的主要阅读方式,某校兴趣小组在全市随机调查了![]() 名居民,经统计这
名居民,经统计这![]() 人中通过电子阅读与纸质阅读的人数之比为
人中通过电子阅读与纸质阅读的人数之比为![]() ,将这
,将这![]() 人按年龄分组,其中统计通过电子阅读的居民得到的频率分布直方图如图所示.
人按年龄分组,其中统计通过电子阅读的居民得到的频率分布直方图如图所示.
(1)求![]() 的值及通过电子阅读的居民的平均年龄;
的值及通过电子阅读的居民的平均年龄;


(2)把年龄在第![]() 组的居民称为青少年组,年龄在第
组的居民称为青少年组,年龄在第![]() 组的居民称为中老年组,若选出的
组的居民称为中老年组,若选出的![]() 人中通过纸质阅读的中老年有
人中通过纸质阅读的中老年有![]() 人,请完成上面
人,请完成上面![]() 列联表,则是否有
列联表,则是否有![]() 的把握认为阅读方式与年龄有关?
的把握认为阅读方式与年龄有关?
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com