
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,倾斜角
,倾斜角
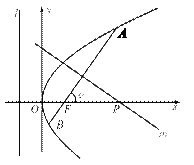
为![]() 的直线经过焦点
的直线经过焦点![]() ,且与抛物线交于
,且与抛物线交于![]() 、
、![]() 两点.
两点.
(1)求抛物线的标准方程及准线![]() 的方程;
的方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 轴于点
轴于点![]() ,证明
,证明![]() 为定值,并求此定值.
为定值,并求此定值.
科目:高中数学 来源: 题型:
【题目】一个袋中装有![]() 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,求取出的两个球编号之和为
次,求取出的两个球编号之和为![]() 的概率.
的概率.
(Ⅱ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,求恰有
次,求恰有![]() 次抽到
次抽到![]() 号球的概率.
号球的概率.
(Ⅲ)若一次从袋中随机抽取![]() 个球,记球的最大编号为
个球,记球的最大编号为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
(Ⅳ)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,记球的最大编号为
次,记球的最大编号为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级设计了一个实验学科的能力考查方案:考生从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题.规定:至少正确完成其中2道题的便可通过该学科的能力考查.已知6道备选题中考生甲能正确完成其中4道题,另2道题不能完成;考生乙正确完成每道题的概率都为![]() .
.
(Ⅰ)分别求考生甲、乙能通过该实验学科能力考查的概率;
(Ⅱ)记所抽取的3道题中,考生甲能正确完成的题数为![]() ,写出
,写出![]() 的概率分布列,并求
的概率分布列,并求![]() 及
及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,曲线
,曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() ;曲线
;曲线![]() 上的点
上的点![]() 在
在![]() 轴的右边且
轴的右边且![]() 到
到![]() 的距离与它到
的距离与它到![]() 轴的距离的差为1.
轴的距离的差为1.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,直线
,直线![]() 分别与
分别与![]() 相交于点
相交于点![]() 和
和![]() .求
.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县城出租车的收费标准是:起步价是![]() 元(乘车不超过
元(乘车不超过![]() 千米);行驶
千米);行驶![]() 千米后,每千米车费1.2元;行驶
千米后,每千米车费1.2元;行驶![]() 千米后,每千米车费1.8元.
千米后,每千米车费1.8元.
(1)写出车费与路程的关系式;
(2)一顾客计划行程![]() 千米,为了省钱,他设计了三种乘车方案:
千米,为了省钱,他设计了三种乘车方案:
①不换车:乘一辆出租车行![]() 千米;
千米;
②分两段乘车:先乘一辆车行![]() 千米,换乘另一辆车再行
千米,换乘另一辆车再行![]() 千米;
千米;
③分三段乘车:每乘![]() 千米换一次车.
千米换一次车.
问哪一种方案最省钱.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为加快新能源汽车产业发展,推进节能减排,国家鼓励消费者购买新能源汽车.某校研究性学习小组从汽车市场上随机选取了M辆纯电动乘用车.根据其续驶里程R(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
分组 | 频数 | 频率 |
80≤R<150 | 10 |
|
150≤R<250 | 30 | x |
R≥250 | y | z |
合计 | M | 1 |
(1)求x,y,z,M的值;
(2)若用分层抽样的方法从这M辆纯电动乘用车中抽取一个容量为6的样本,从该样本中任选2辆,求选到的2辆车续驶里程为150≤R<250的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com