(1)解方程:log2(9x-5)=log2(3x-2)+2;
(2)已知:0≤x<2π,解方程:cos2x=cosx(sinx+|sinx|).
解:(1)∵log
2(9
x-5)=log
2(3
x-2)+2,∴log
2(9
x-5)=log
2[4(3
x-2)],∴9
x-5=4•3
x-8,
即(3
x)
2-4•3
x+3=0解得:3
x=3 或 3
x=1,故 x
1=1,x
2=0.
经检验:x=1是原方程的根.
(2)由已知0≤x<2π,
①当0≤x≤π时,sinx≥0,cos2x=cosx(sinx+|sinx|)可化为:cos2x=sin2x,tan2x=1,∴

或=

.
②当π<x<2π时,sinx<0,cos2x=cosx(sinx+|sinx|)可化为:cos2x=0,∴
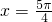
或
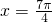
.
综上:原方程的解集为

.
分析:(1)由方程 9
x-5=4•3
x-8,即(3
x)
2-4•3
x+3=0解得:3
x=3 或 3
x=1,由此解指数方程求得x的值,注意验根.
(2)①当0≤x≤π时,sinx≥0,方程化为 tan2x=1,求得x的值.②当π<x<2π时,sinx<0,方程化为cos2x=0,求得x的值.所有的x值组成的集合就是所求.
点评:本题主要考查对数函数的定义域,对数方程的解法,根据三角函数的值求角,体现了等价转化和分类讨论的数学思想.

 或=
或= .
.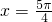 或
或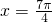 .
. .
.

![]()
![]() ,则方程f ( x ) = 1的解集是
,则方程f ( x ) = 1的解集是