
【题目】已知定义在R上的函数f(x)=2x﹣ ![]() .
.
(1)若f(x)= ![]() ,求x的值;
,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
【答案】
(1)解:由题意:f(x)=2x﹣ ![]() 定义在R上的函数,
定义在R上的函数,
∴ 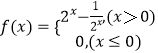
当x≤0时,f(x)=0,无解
当x>0时,f(x)=2x﹣ ![]() ,
,
由f(x)= ![]() ,即:2x﹣
,即:2x﹣ ![]() =
= ![]() ,
,
化简:222x﹣32x﹣2=0
因式分解:(2x﹣2)(22x+2)=0
解得:解得2x=2或2x=﹣ ![]() ,
,
∵2x>0,
故:x=1
(2)解:当t∈[1,2]时,
f(2t)= ![]() ,f(t)=
,f(t)= ![]()
那么: ![]() (
( ![]() )≥0
)≥0
整理得:m(22t﹣1)≥﹣(24t﹣1)
∵22t﹣1>0,∴m≥﹣(22t+1)恒成立即可.
∵t∈[1,2],∴﹣(22t+1)∈[﹣17,﹣5].
要使m≥﹣(22t+1)恒成立,只需m≥﹣5
故:m的取值范围是[﹣5,+∞)
【解析】(1)化简f(x)去掉绝对值,直接进行带值计算即可.(2)求出f(2t),f(t)带入,构造指数函数,利用指数函数的图象及性质对t∈[1,2]恒成立求解.
【考点精析】本题主要考查了函数单调性的判断方法的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能正确解答此题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】下列各小题中,P是q的充要条件的是(08年山东理改编)
1)p:m<﹣2或m>6;q:y=x2+mx+m+3有两个不同的零点.
2)p: ![]() =1,q:y=f(x)是偶函数.
=1,q:y=f(x)是偶函数.
3)p:cosα=cosβ,q:tanα=tanβ.
4)p:A∩B=A,q:CUBCUA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() (a>0,b>0).
(a>0,b>0).
(1)当a=b=1时,证明:f(x)不是奇函数;
(2)设f(x)是奇函数,求a与b的值;
(3)在(2)的条件下,试证明函数f(x)的单调性,并解不等式f(1﹣m)+f(1+m2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2+a|x|+2,x∈R在区间[3,+∞)和[﹣2,﹣1]上均为增函数,则实数a的取值范围是( )
A.[﹣ ![]() ,﹣3]
,﹣3]
B.[﹣6,﹣4]
C.[﹣3,﹣2 ![]() ]
]
D.[﹣4,﹣3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(0)=2和f(x+1)﹣f(x)=2x﹣1对任意实数x都成立.
(1)求函数f(x)的解析式;
(2)当t∈[﹣1,3]时,求y=f(2t)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=﹣x与直线y=k(x+1)(k≠0)相交于A、B两点,O是坐标原点.
(1)当k= ![]() 时,求|AB|的长;
时,求|AB|的长;
(2)求证无论k为何值都有OA⊥OB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 过点
过点![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率
,离心率![]() ,
, ![]() 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且![]() .
.
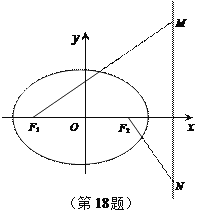
(1)求椭圆的方程;
(2)求![]() 的最小值;
的最小值;
(3)以![]() 为直径的圆
为直径的圆![]() 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(1﹣x)+loga(x+3),(0<a<1).
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣2,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com