
已知函数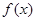 是定义在
是定义在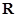 上的偶函数,且当
上的偶函数,且当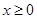 时,
时,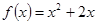 .
.
(1)写出函数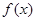 在
在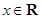 的解析式;
的解析式;
(2)若函数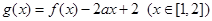 ,求函数
,求函数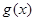 的最小值.
的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=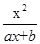 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)< 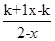 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中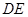 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,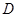 在
在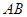 上,
上,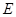 在
在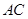 上.
上.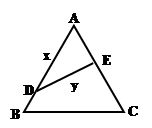
(1)设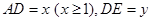 ,求用
,求用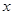 表示
表示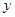 的函数关系式;
的函数关系式;
(2)如果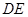 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,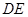 的位置应在哪里?如果
的位置应在哪里?如果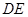 是参观线路,则希望它最长,
是参观线路,则希望它最长,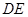 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少.从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.
(1)求第n年初M的价值an的表达式;
(2)求数列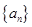 的前n项和
的前n项和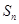
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产1百件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为5百件,产品销售数量为t(百件)时,销售所得的收入为(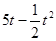 )万元。
)万元。
(1)该公司这种产品的年生产量为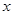 百件,生产并销售这种产品得到的利润为当年产量
百件,生产并销售这种产品得到的利润为当年产量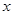 的函数
的函数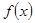 ,求
,求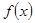 ;
;
(2)当该公司的年产量为多大时当年所获得的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为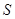 平方米.
平方米.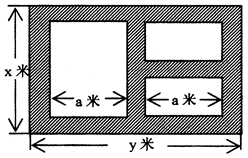
(1)分别写出用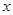 表示
表示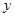 和用
和用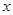 表示
表示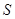 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某房地产开发商投资81万元建一座写字楼,第一年维修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。(1)n年利润是多少?第几年该楼年平均利润最大?最大是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
建造一断面为等腰梯形的防洪堤(如图),梯形的腰与底边所角为60°,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为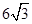 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com