
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)设椭圆右焦点![]() 的坐标为
的坐标为![]() ,由
,由![]() ,可得
,可得![]() ,又
,又![]() ,即可求解椭圆的离心率;(2)由(1)知
,即可求解椭圆的离心率;(2)由(1)知![]() ,得到椭圆的方程为
,得到椭圆的方程为![]() ,设出点
,设出点![]() ,可得
,可得![]() ,进而得到
,进而得到![]() ,由于点
,由于点![]() 在椭圆上,联立得到
在椭圆上,联立得到![]() ,解得
,解得![]() ,利用中点公式和两点间的距离公式,利用直线与圆相切的性质即可得出结论.
,利用中点公式和两点间的距离公式,利用直线与圆相切的性质即可得出结论.
试题解析:(1)设椭圆右焦点![]() 的坐标为
的坐标为![]() ,由
,由![]() ,可得
,可得![]() .
.
又![]() ,则
,则![]() ,所以椭圆的离心率
,所以椭圆的离心率![]() .
.
(2)由(1)知![]() ,故椭圆的方程为
,故椭圆的方程为![]() ,
,
设![]() ,由
,由![]() ,有
,有![]() ,
,
由已知,有![]() ,即
,即![]() ,又
,又![]() ,故有
,故有![]() . ①
. ①
又因为点![]() 在椭圆上,所以
在椭圆上,所以![]() .②
.②
由 ①和②可得![]() ,而点
,而点![]() 不是椭圆的顶点,故
不是椭圆的顶点,故![]() ,
,
代人①得![]() ,即点
,即点![]() 的坐标为
的坐标为![]() ,设圆的圆心为
,设圆的圆心为![]() ,
,
则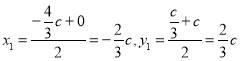 ,进而圆的半径
,进而圆的半径![]() ,
,
设直线![]() 的斜率为
的斜率为![]() ,依题意,直线
,依题意,直线![]() 的方程
的方程![]() .由
.由![]() 与圆相切,可得
与圆相切,可得![]() ,
,
即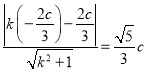 ,整理得
,整理得![]() ,解得
,解得![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() 或
或![]() .
.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系,![]() 点的极坐标为
点的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为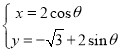 (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护环境,2015年合肥市胜利工厂在市政府的大力支持下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本![]() (万元)与处理量
(万元)与处理量![]() (吨)之间的函数关系可近似地表示为:
(吨)之间的函数关系可近似地表示为: 且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(1)当![]() 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,点
,点![]() 为坐标原点,若椭圆
为坐标原点,若椭圆![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() (
(![]() 下
下![]() 上),且
上),且![]() 两点满足
两点满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 上异于其顶点的任一点
上异于其顶点的任一点![]() ,作
,作![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,且直线
,且直线![]() 在
在![]() 轴、
轴、![]() 轴上的截距分别为
轴上的截距分别为![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市有一直角梯形绿地![]() ,其中
,其中![]() ,
,![]() km,
km,![]() km.现过边界
km.现过边界![]() 上的点
上的点![]() 处铺设一条直的灌溉水管
处铺设一条直的灌溉水管![]() ,将绿地分成面积相等的两部分.
,将绿地分成面积相等的两部分.
(1)如图①,若![]() 为
为![]() 的中点,
的中点,![]() 在边界
在边界![]() 上,求灌溉水管
上,求灌溉水管![]() 的长度;
的长度;
(2)如图②,若![]() 在边界
在边界![]() 上,求灌溉水管
上,求灌溉水管![]() 的最短长度.
的最短长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在冬季供暖时减少能量损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位:![]() )满足关系:
)满足关系:![]() ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中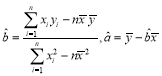 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com