
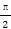 ).
). ⊥a,且|
⊥a,且| |=
|=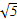 |
| |(O为坐标原点),求向量
|(O为坐标原点),求向量 .
. 与向量a共线,当k>4,且tsinθ取最大值4时,求
与向量a共线,当k>4,且tsinθ取最大值4时,求 ·
· .
. =(24,8)或
=(24,8)或 =(-8,-8) (2) 32
=(-8,-8) (2) 32 =(n-8,t),
=(n-8,t), ⊥a,∴
⊥a,∴ ·a=(n-8,t)·(-1,2)=0,
·a=(n-8,t)·(-1,2)=0, =(2t,t).
=(2t,t). |=
|=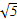 |
| |,|
|,| |=8.
|=8. =(24,8)或
=(24,8)或 =(-8,-8).
=(-8,-8). 与向量a共线,
与向量a共线, )2+
)2+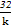 .
. <1,故当sinθ=
<1,故当sinθ= 时,tsinθ取最大值
时,tsinθ取最大值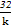 ,有
,有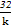 =4,得k=8.
=4,得k=8. ,k=8,tsinθ=4,得t=8,
,k=8,tsinθ=4,得t=8, =(4,8),
=(4,8), ·
· =(8,0)·(4,8)=32.
=(8,0)·(4,8)=32.

科目:高中数学 来源:不详 题型:填空题
 =
= ,且|
,且| |=|
|=| |;
|; +
+ +
+ =0;
=0; =3e1,
=3e1, =-5e1,且|
=-5e1,且| |=|
|=| |,则四边形ABCD是等腰梯形;
|,则四边形ABCD是等腰梯形; |=8,|
|=8,| |=5,则3≤|
|=5,则3≤| |≤13.
|≤13.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com