
分析 (1)设直线$AB:x=my+\frac{1}{6}$,将直线AB与抛物线联立,设A(x1,y1),B(x2,y2),由韦达定理业绩向量关系,求解直线的斜率即可.
(2)利用三角形的面积公式以及弦长公式,结合二次函数的性质求解函数的最小值即可.
解答 (12分)解:(1)依题意可设直线$AB:x=my+\frac{1}{6}$,
将直线AB与抛物线联立$\left\{\begin{array}{l}x=my+\frac{1}{6}\\{y^2}=\frac{2}{3}x\end{array}\right.$⇒9y2-6my-1=0
设A(x1,y1),B(x2,y2),由韦达定理得$\left\{\begin{array}{l}{y_1}+{y_2}=\frac{2}{3}m\\{y_1}{y_2}=-\frac{1}{9}\end{array}\right.$
∵$\overrightarrow{AF}=3\overrightarrow{FB}⇒{y_1}=-3{y_2}$,$⇒{m^2}=\frac{1}{3}$,
∴斜率为$\sqrt{3}$或$-\sqrt{3}$.-------(6分)
(2)${S_{OACB}}=2{S_{△AOB}}=2•\frac{1}{2}|{OF}||{{y_1}-{y_2}}|=\frac{1}{6}×|{{y_1}-{y_2}}|=\frac{1}{6}\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}=\frac{1}{6}\sqrt{\frac{4}{9}{m^2}+\frac{4}{9}}≥\frac{1}{6}×\frac{2}{3}=\frac{1}{9}$
当m=0时,四边形OACB的面积最小,最小值为$\frac{1}{9}$.-------(12分)
点评 本题考查直线与抛物线的位置关系的应用,设而不求以及二次函数的性质的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,0) | B. | (0,3) | C. | $(\sqrt{3},0)$ | D. | $(0,\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 2月1日 | 2月2日 | 2月3日 | 2月4日 | 2月5日 |
| 温差x(°C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数x(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
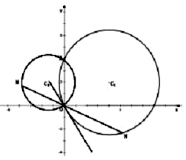 已知圆${C_1}:{({x-4})^2}+{({y-2})^2}=20$与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
已知圆${C_1}:{({x-4})^2}+{({y-2})^2}=20$与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 8 | C. | $\sqrt{17}-1$ | D. | $\sqrt{15}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
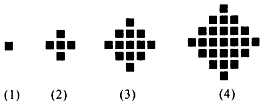 某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | $(\frac{1}{16},0)$ | C. | $(0,\frac{1}{16})$ | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com