
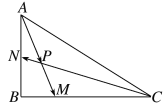
【题目】在△ABC中,![]() .
.
(1)求△ABM与△ABC的面积之比;
(2)若N为AB中点,![]() 与
与![]() 交于点P,且
交于点P,且![]() (x,y∈R),求x+y的值.
(x,y∈R),求x+y的值.
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2+bx+c(a>0),
(1)当a=1,b=2,若|f(x)|﹣2=0有且只有两个不同的实根,求实数c的取值范围;
(2)设方程f(x)=x的两个实根为x1 , x2 , 且满足0<t<x1 , x2﹣x1> ![]() ,试判断f(t)与x1的大小,并给出理由.
,试判断f(t)与x1的大小,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地环保部门跟踪调查一种有害昆虫的数量.根据调查数据,该昆虫的数量![]() (万只)与时间
(万只)与时间![]() (年)(其中
(年)(其中![]() )的关系为
)的关系为![]() .为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值
.为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值![]() (其中
(其中![]() 为常数,且
为常数,且![]() )来进行生态环境分析.
)来进行生态环境分析.
(1)当![]() 时,求比值
时,求比值![]() 取最小值时
取最小值时![]() 的值;
的值;
(2)经过调查,环保部门发现:当比值![]() 不超过
不超过![]() 时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数
时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底,
为自然对数的底, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了普及奥运会知识和提高学生参加体育运动的积极性,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.
(Ⅰ)在这30名学生中,甲组学生中有男生7人,乙组学生中有女生12人,试问有没有90%的把握认为成绩分在甲组或乙组与性别有关;
(Ⅱ)记甲组学生的成绩分别为x1 , x2 , …,x12 , 执行如图所示的程序框图,求输出的S的值;
(Ⅲ)竞赛中,学生小张、小李同时回答两道题,小张答对每道题的概率均为 ![]() ,小李答对每道题的概率均为
,小李答对每道题的概率均为 ![]() ,两人回答每道题正确与否相互独立.记小张答对题的道数为a,小李答对题的道数为b,X=|a﹣b|,写出X的概率分布列,并求出X的数学期望.
,两人回答每道题正确与否相互独立.记小张答对题的道数为a,小李答对题的道数为b,X=|a﹣b|,写出X的概率分布列,并求出X的数学期望.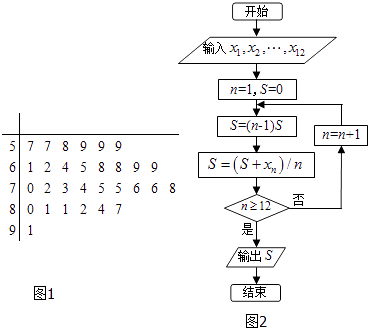
附:K2= ![]() ;其中n=a+b+c+d
;其中n=a+b+c+d
独立性检验临界表:
P(K2>k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)记F(x)=f(x)﹣g(x),判断F(x)在区间(1,2)内零点个数并说明理由;
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并给出对应的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分8分)某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.

(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在[50,60)∪[90,100]内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“|m﹣n|>10”概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了普及奥运会知识和提高学生参加体育运动的积极性,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.
(Ⅰ)在这30名学生中,甲组学生中有男生7人,乙组学生中有女生12人,试问有没有90%的把握认为成绩分在甲组或乙组与性别有关;
(Ⅱ)记甲组学生的成绩分别为x1 , x2 , …,x12 , 执行如图所示的程序框图,求输出的S的值;
(Ⅲ)竞赛中,学生小张、小李同时回答两道题,小张答对每道题的概率均为 ![]() ,小李答对每道题的概率均为
,小李答对每道题的概率均为 ![]() ,两人回答每道题正确与否相互独立.记小张答对题的道数为a,小李答对题的道数为b,X=|a﹣b|,写出X的概率分布列,并求出X的数学期望.
,两人回答每道题正确与否相互独立.记小张答对题的道数为a,小李答对题的道数为b,X=|a﹣b|,写出X的概率分布列,并求出X的数学期望.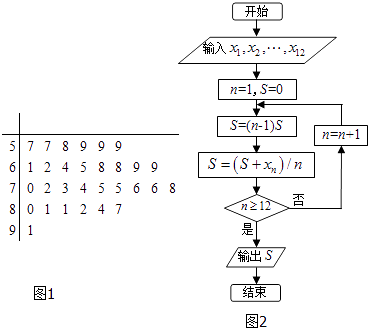
附:K2= ![]() ;其中n=a+b+c+d
;其中n=a+b+c+d
独立性检验临界表:
P(K2>k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com