
【题目】(本题![]() 分)
分)
已知定义在![]() 上的两个函数
上的两个函数![]() ,
, ![]() 图象有公共点,且在公共点处的切线相同.
图象有公共点,且在公共点处的切线相同.
(Ⅰ)用![]() 表示
表示![]() .
.
(Ⅱ)求证: ![]() .
.
【答案】详见解析
【解析】试题分析:(Ⅰ)设出两曲线的公共点坐标,分别求出f(x)和g(x)的导函数,把设出点的坐标代入两导函数中得到两关系式,联立两关系式即可解出公共点的横坐标,把求出的横坐标代入得到用a表示出b的式子;
(Ⅱ)设F(x)=f(x)﹣g(x),求出F(x)的导函数,根据导函数的正负得到F(x)的单调区间,由x大于0和函数的增减性得到F(x)的最小值为0,即f(x)﹣g(x)大于等于0,得证.
试题解析:
(Ⅰ)设![]() 与
与![]() 公共点
公共点![]() 处的切线相同.
处的切线相同.
∵![]() ,
, ![]() ,
,
由题意![]() ,
, ![]() ,
,
即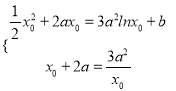 ,
,
得![]() 或
或![]() (舍去),
(舍去),
即有![]() .
.
(Ⅱ)证明:设![]() ,
,
则![]() ,
, ![]() ,
,
故![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,
为增函数,
所以函数![]() 在
在![]() 上有最小值,
上有最小值, ![]() ,
,
故当![]() 时,有
时,有![]() ,
,
即当![]() 时,
时, ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为2的圆内有两条圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度![]() 的图像大致为( )
的图像大致为( )


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·武昌调研)如图,在圆内画1条线段,将圆分成2部分;画2条相交线段,将圆分割成4部分;画3条线段,将圆最多分割成7部分;画4条线段,将圆最多分割成11部分.则
![]()
(1)在圆内画5条线段,将圆最多分割成________部分;
(2)在圆内画n条线段,将圆最多分割成________部分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲乙丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )
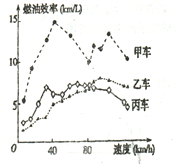
A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比乙车更省油.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P—A1B1C1D1,下部的形状是正四棱柱ABCD—A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
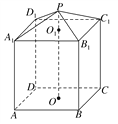
(1)若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为6 m,则当PO1为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A是x轴正半轴上的任一点,且![]() ,点B在射线ON上运动.
,点B在射线ON上运动.
(1)若点![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的值;
的值;
(2)若点![]() ,求点A关于射线
,求点A关于射线![]() 的对称点P的坐标;
的对称点P的坐标;

(3)若![]() ,C为线段AB的中点,若Q为点C关于射线ON的对称点,求点
,C为线段AB的中点,若Q为点C关于射线ON的对称点,求点![]() 的轨迹方程,并指出x、y的取值范围.
的轨迹方程,并指出x、y的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AD∥BC,CD⊥BC,AD=2,AB=BC=3,PA=4,M为AD的中点,N为PC上一点,且PC=3PN.
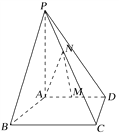
(1)求证:MN∥平面PAB;
(2)求点M到平面PAN的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为
的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,若点
,若点![]() 总在以线段
总在以线段![]() 为直径的圆内,求
为直径的圆内,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com