
分析 (I)利用递推关系即可得出;
(II)利用对数的运算性质、等差数列的求和公式可得bn,代入利用二次函数的单调性即可得出.
解答 解:(Ⅰ)∵${S}_{n}={2}^{n+1}-2$.∴n=1时,a1=2.
n≥2时,an=Sn-Sn-1=2n+1-2-(2n-2)=2n,n=1时也成立.
∴an=2n.
(Ⅱ)bn=log2a1+log2a2+…+log2an=$lo{g}_{2}({2}^{1+2+…+n})$=$\frac{n(n+1)}{2}$,
(n-8)bn≥nk,即(n-8)×$\frac{n(n+1)}{2}$≥nk,化为:k≤$\frac{(n-8)(n+1)}{2}$,
而f(n)=$\frac{(n-8)(n+1)}{2}$=$\frac{1}{2}(n-\frac{7}{2})^{2}$-$\frac{77}{8}$,
当n=3或4时,f(n)取得最小值,f(3)=-10.
∴使(n-8)bn≥nk对任意n∈N+恒成立的实数k的取值范围是(-∞,-10].
点评 本题考查了数列递推关系、等差数列的定义通项公式及其求和公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
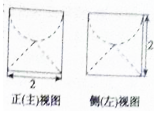 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )| A. | (4+$\sqrt{2}$)π | B. | 6$π+2\sqrt{2}π$ | C. | 6$π+\sqrt{2}π$ | D. | (8+$\sqrt{2}$)π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
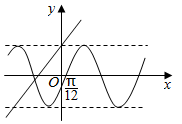 若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )
若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )| A. | x=-$\frac{π}{24}$ | B. | x=$\frac{37π}{24}$ | C. | x=$\frac{17π}{24}$ | D. | x=-$\frac{13π}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com