
【题目】按照国家环保部发布的新修订的《环境空气质量标准》,规定:PM2.5的年平均浓度不得超过35微克/立方米,国家环保部门在2016年10月1日到2017年1月30日这120天对全国的PM2.5平均浓度的监测数据统计如下:
组别 | PM2.5浓度(微克/立方米) | 频数(天) |
第一组 |
| 32 |
第二组 |
| 64 |
第三组 |
| 16 |
第四组 | 115以上 | 8 |
(1)在这120天中抽取30天的数据做进一步分析,每一组应抽取多少天?
(2)在(1)中所抽取的样本PM2.5的平均浓度超过75(微克/立方米)的若干天中,随机抽取2天,求恰好有一天平均浓度超过115(微克/立方米)的概率.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)本问考查分层抽样,根据各组频数可知,比例关系为32:64:16:8=4:8:2:1,所以根据比例关系可知,若从120天中抽取30天做进一步分析,各组依次应抽取的天数分别为8天,16天,4天,2天;(2)本问考查古典概型概率问题,PM2.5浓度超过75(微克/立方米)的共6天,其中在![]() 的有4天,编号为
的有4天,编号为![]() ,浓度在115以上的有2天,编号为
,浓度在115以上的有2天,编号为![]() ,随机抽取2天,写出基本事件空间,找出恰好有一天平均浓度超过115所包含的基本事件个数,即可以求出概率.
,随机抽取2天,写出基本事件空间,找出恰好有一天平均浓度超过115所包含的基本事件个数,即可以求出概率.
试题解析:(Ⅰ)这120天中抽取30天,应采取分层抽样,
第一组抽取![]() 天;第二组抽取
天;第二组抽取![]() 天;
天;
第三组抽取![]() 天;第四组抽取
天;第四组抽取![]() 天.
天.
(Ⅱ)设PM2.5的平均浓度在![]() 内的4天记为
内的4天记为![]() ,PM2.5的平均浓度在115以上的两天记为
,PM2.5的平均浓度在115以上的两天记为![]() .
.
所以6天任取2天的情况有:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 共15种.
共15种.
记“恰好有一天平均浓度超过115(微克/立方米)”为事件![]() ,其中符合条件的有:
,其中符合条件的有:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 共8种,
共8种,
所求事件A的概率:![]()


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】设直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称.
对称.
(1)求m,k的值;
(2)若直线![]() 与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线![]() 对称的圆的方程;
对称的圆的方程;
(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点![]() ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.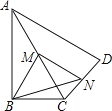
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为
②该函数的一条性质:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() 为参数). 点
为参数). 点![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
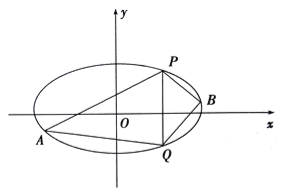
【题目】【天津市红桥区重点中学八校2017届高三4月联考数学(文)】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点
的焦点
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点, ![]() ,
, ![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.①若直线
两侧的动点.①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() ,
, ![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com