
(本小题满分14分)设函数f(x)=x2+aln(x+1).
(1)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;
(2)若函数y=f(x)有两个极值点x1,x2,且x1<x2,求证: .
.
(1)[-4,+∞);(2)见解析
【解析】
试题分析:(1)根据f '(x)≥0在区间[1,+∞)上恒成立,可求得a的取值范围;(2)现根据f '(x)=0,找到x1,x2的关系,将 转换为一个字母x2的函数式,然后利用x2的范围,利用函数的单调性找到最值,即可求出
转换为一个字母x2的函数式,然后利用x2的范围,利用函数的单调性找到最值,即可求出 的范围.
的范围.
试题解析:(1)由题意,f '(x)= ≥0在区间[1,+∞)上恒成立
≥0在区间[1,+∞)上恒成立
即a≥-2x2-2x在区间[1,+∞)上恒成立
而-2x2-2x在区间[1,+∞)上的最大值为-4
故a≥-4
经检验,当a=-4时,f '(x)=
当x∈[1,+∞)时,f '(x)≥0,所以满足题意的a的取值范围是[-4,+∞)
(2)函数的定义域为(-1,+∞),f '(x)=
依题意,方程2x2+2x+a=0在区间(-1,+∞)上有两个不相等的实根
记g(x)=2x2+2x+a
则有 ,解得0<a<
,解得0<a<
x2为方程2x2+2x+a=0的解,∴a=-2x22-2x2.
∵0<a< ,x1<x2<0,x2=-
,x1<x2<0,x2=- ,∴-
,∴- <x2<0,从而x1<0
<x2<0,从而x1<0
先证 >0,因为x1<x2<0,即证f(x2)<0
>0,因为x1<x2<0,即证f(x2)<0
∵在区间(x1,x2)内,f '(x)<0,在区间(x2,0)内,f '(x)>0
∴f(x2)为极小值,f(x2)<f(0)=0
∴ >0成立.
>0成立.
再证 +ln2,
+ln2,
即证f(x2)>(- +ln2)(-1-x2)=(
+ln2)(-1-x2)=( -ln2)(x2+1)
-ln2)(x2+1)

令g(x)= ,x∈(-
,x∈(- ,0)
,0)
g'(x)=2x-(4x+2)ln(x+1)- -ln2)
-ln2)
=-2(2x+1)ln(x+1)-( -ln2)
-ln2)
又ln(x+1)<0,2x+1>0, -ln2<0
-ln2<0
∴g'(x)>0,即g(x)在(- ,0)上是增函数
,0)上是增函数
g(x)>g(- )=
)=
=
= -ln2
-ln2
综上可得, 成立
成立
考点:利用导数研究函数性质,函数的单调性,极值,方程,不等式


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:解答题
某校高三年级文科学生600名,从参加期末考试的学生中随机抽出某班学生(该班共50名同学),并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下表:
分组 | 频数 | 频率 |
[45,60) | 2 | 0.04 |
[60,75) | 4 | 0.08 |
[75,90) | 8 | 0.16 |
[90,105) | 11 | 0.22 |
[105,120) | 15 | 0.30 |
[120,135) | a | b |
[135,150] | 4 | 0.08 |
合计 | 50 | 1 |
(1)写出a、b的值;
(2)估计该校文科生数学成绩在120分以上学生人数;
(3)该班为提高整体数学成绩,决定成立“二帮一”小组,即从成绩在[135,150]中选两位同学,来帮助成绩在[45,60)中的某一位同学.已知甲同学的成绩为56分, 乙同学的成绩为145分,求甲乙在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源:2015届四川省高三10月月考理科数学试卷(解析版) 题型:选择题
某程序框图如图所示,若使输出的结果不大于 37,则输入的整数i的最大值为( )

A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知锐角△ABC中的三个内角分别为A,B,C.
(1)设 ,求证△ABC是等腰三角形;
,求证△ABC是等腰三角形;
(2)设向量s=(2sinC,- ),t=(cos2C,2
),t=(cos2C,2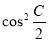 -1),且s∥t,若sinA=
-1),且s∥t,若sinA=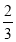 ,求sin(
,求sin( -B)的值.
-B)的值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:选择题
已知双曲线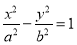 (a>0,b>0)的右焦点为F(2,0),设A,B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,若直线AB斜率为
(a>0,b>0)的右焦点为F(2,0),设A,B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,若直线AB斜率为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A、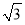 B、
B、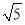 C、2 D、4
C、2 D、4
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:填空题
已知抛物线y2=2px(p>0)的准线与直线x+y-3=0以及x轴围成三角形面积为8,则p=__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com