
【题目】已知三棱锥的两条棱长为1,其余四条棱长为2,有下列命题:
![]() 该三棱锥的体积是
该三棱锥的体积是![]() ;
;
![]() 该三棱锥内切球的半径是
该三棱锥内切球的半径是![]() ;
;
![]() 该三棱锥外接球的表面积是
该三棱锥外接球的表面积是![]() .
.
其中正确的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
三棱锥![]() 中,
中,![]() ,
,![]() ,取BC,PA的中点D,E,①利用过BC中点D与BC垂直的截面三角形PAD为底,以BC高求得体积,验证正确;
,取BC,PA的中点D,E,①利用过BC中点D与BC垂直的截面三角形PAD为底,以BC高求得体积,验证正确;
②利用四面全等,由内切球球心为顶点把三棱锥等分四份,不难求得半径r,验证正确;
③首先确定DE中点为外接球球心,不难求解,验证错误.
如图所示,三棱锥![]() 中
中
![]() ,
,![]() ,
,
取BC,PA的中点D,E,作如图的连接
则![]() ,
,![]() ,
,
![]() 平面PAD
平面PAD
并求得:![]() ;
;
![]() ,
,
![]() 三棱锥
三棱锥![]() 的体积为
的体积为![]() ,
,![]() 正确;
正确;
设内切球的半径为r,球心为M,
显然四个面三角形全等![]() ,
,
解得![]() ,
,![]() 正确;
正确;
事实上,外接球球心O必在过D点与BC垂直的平面PAD内,
和过E点与PA垂直的平面BCE内,
故O点在平面PAD和平面BCE的交线DE上,
在![]() 内,
内,![]()
同样,在![]() 内,
内,![]()
![]() ≌
≌![]()
![]() ,即O为DE的中点,
,即O为DE的中点,
可求得外接球半径R的平方:![]() 故
故![]() 错误
错误
故选:B.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为![]() .
.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:

将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
(1)根据已知条件完成下面的![]() 列联表,并据此资料我们能否有
列联表,并据此资料我们能否有![]() 的把握认为“歌迷”与性别有关?
的把握认为“歌迷”与性别有关?

(2)将收看该节目所有场次(14场)的观众称为“超级歌迷”,已知“超级歌迷”中有2名女性,若从“超级歌迷”中任意选取2人,求至少有1名女性观众的概率.

附: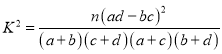 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (其中
(其中![]() 为参数).现以坐标原点为极点,
为参数).现以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 普通方程和曲线
普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() ,且与直线
,且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是( )
.下列结论正确的是( )
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线
,在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 求曲线
求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若射线l:
若射线l:![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为A,
的交点分别为A,![]() B异于原点
B异于原点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点为极点,
).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动点,若点
上的一个动点,若点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() ,求
,求![]() 的值;
的值;
(2)若曲线![]() 上任意一点
上任意一点![]() 都满足
都满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
(1)请先求出频率分布表中①、②位置的相应数据,再完成如下的频率分布直方图;

(2)组委会决定在5名(其中第3组2名,第4组2名,第5组1名)选手中随机抽取2名选接受![]() 考官进行面试,求第4组至少有1名选手被考官
考官进行面试,求第4组至少有1名选手被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的PK赛,![]() 两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为
两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com