
【题目】如图所示,B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD,△BCD的重心.

(1)求证:平面MNG∥平面ACD;
(2)求![]()
【答案】⑴见证明;⑵ 1∶9
【解析】
(1)利用三角形重心的性质,结合线面平行的判定定理,证明MN∥平面ACD,MG∥平面ACD,再证明平面MNG∥平面ACD;
(2)证明![]() ,其相似比为1∶3,可得结论.
,其相似比为1∶3,可得结论.
⑴连接BM,BN,BG并延长分别交AC,AD,CD于P,F,H.
∵M,N,G分别为△ABC,△ABD,△BCD的重心,
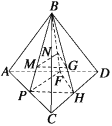
则有![]()
且P,H,F分别为AC,CD,AD的中点.
连接PF,FH,PH,有MN∥PF.
又PF平面ACD,MN平面ACD,
∴MN∥平面ACD.
同理MG∥平面ACD,MG∩MN=M,
∴平面MNG∥平面ACD.
(2)解 由(1)可知![]()
![]() ,
,
又![]() ,∴
,∴![]() .
.
同理![]() ,
,![]()
![]() ,其相似比为1∶3.
,其相似比为1∶3.
∴S△MNG∶S△ACD=1∶9.


科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在R上为增函数,且f(1)= ![]() ,若实数a满足f(loga3)﹣f(loga
,若实数a满足f(loga3)﹣f(loga ![]() )≤1,则实数a的取值范围为( )
)≤1,则实数a的取值范围为( )
A.0<a≤ ![]()
B.a≤ ![]()
C.![]() ≤a<1
≤a<1
D.a≥3或0<a<1
查看答案和解析>>
科目:高中数学 来源: 题型:
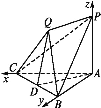
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC是直角三角形,且PA=AB=AC.又平面QBC垂直于底面ABC.
(1)求证:PA∥平面QBC;
(2)若PQ⊥平面QBC,求锐二面角Q-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点.
(1)证明:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面DAE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划2011年在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司每分钟所做的广告,能给公司带来的收益分别为0.3 万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下: 
(Ⅰ)记A表示时间“旧养殖法的箱产量低于50kg”,估计A的概率;
(Ⅱ)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(Ⅲ)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
P(K2≥K) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com