
| A. | $2±\sqrt{2}$ | B. | $3±2\sqrt{2}$ | C. | $4±2\sqrt{3}$ | D. | $4±2\sqrt{2}$ |
分析 求出抛物线的焦点,设直线l为x=my+1,代入抛物线方程,运用韦达定理和向量的坐标表示,解得m,再由三角形的面积公式,计算即可得到.
解答 解:抛物线y2=4x的焦点为(1,0),
设直线l为x=my+1,代入抛物线方程可得y2-4my-4=0,
设A(x1,y1),B(x2,y2),
则y1+y2=4m,y1y2=-4,
设$\overline{AF}$=t$\overrightarrow{FB}$,可得y1=-ty2,
由代入法,可得y1=-$\frac{4mt}{1-t}$,y2=$\frac{4m}{1-t}$,m2=$\frac{(1-t)^{2}}{4t}$
∵△AOB的面积为$2\sqrt{2}$,
∴$\frac{1}{2}•1•$|-$\frac{4mt}{1-t}$-$\frac{4m}{1-t}$|=$2\sqrt{2}$,
化简可得t2-6t+1=0,
∴t=3±2$\sqrt{2}$,
故选:B.
点评 本题考查直线和抛物线的位置关系的综合应用,主要考查韦达定理和向量的共线的坐标表示,考查运算能力,属于中档题.


科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
已知复数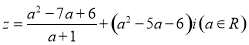 .试求实数
.试求实数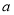 分别为什么值时,
分别为什么值时,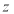 分别为:(1)实数;(2)虚数;(3)纯虚数.
分别为:(1)实数;(2)虚数;(3)纯虚数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
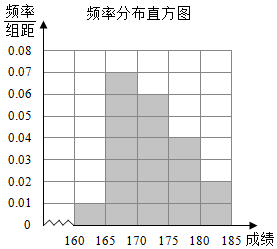 某高校在2015年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示
某高校在2015年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:选择题
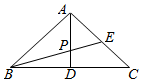 如图,等腰直角三角形ABC中,∠BAC=90°,D为BC的中点,BE平分∠ABC,AD与BE交于点P,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ等于( )
如图,等腰直角三角形ABC中,∠BAC=90°,D为BC的中点,BE平分∠ABC,AD与BE交于点P,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ等于( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{2-\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S2 | B. | 3S2 | C. | 9S2 | D. | 9S2-6S+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com