
(1)求证:直线OA与直线OB不垂直;
(2)如果点E(8,0)在以线段AB为直径的圆上,求直线l的方程.
答案:(1)证明:设A(x1,y1),B(x2,y2),则y12=4x1,y22=4x2,
![]() =(x1-2,y1),
=(x1-2,y1),![]() =(x2-2,y2),∵P、A、B共线,∴
=(x2-2,y2),∵P、A、B共线,∴![]() ∥
∥![]() .
.
∴(x1-2)y2-y1(x2-2)=0.由y12=4x1,y22=4x2得x1=![]() ,x2=
,x2=![]() ,
,
代入(x1-2)y2-y1(x2-2)=0,化简得y1y2=-8.
∵![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),∴x1x2+y1y2=
=(x2,y2),∴x1x2+y1y2=![]() +y1y2=-4≠0.
+y1y2=-4≠0.
∴![]() 与
与![]() 不垂直.∴直线OA与直线OB不垂直.
不垂直.∴直线OA与直线OB不垂直.
(2)解:∵![]() =(x1-8,y1),
=(x1-8,y1),![]() =(x2-8,y2),由点E(8,0)在以线段AB为直径的圆上得
=(x2-8,y2),由点E(8,0)在以线段AB为直径的圆上得![]() ⊥
⊥![]() .
.
∴(x1-8)(x2-8)+y1y2=0.
将x1=![]() ,x2=
,x2=![]() ,y1y2=-8代入(x1-8)(x2-8)+y1y2=0.∴y12+y22=30.
,y1y2=-8代入(x1-8)(x2-8)+y1y2=0.∴y12+y22=30.
∴y1+y2=±![]() =±
=±![]() .
.
∴直线AB的斜率存在,设其为k,则k=![]() =±
=±![]() .
.
∴直线AB的方程为y=±![]() (x-2).
(x-2).
∴当点E(8,0)在以线段AB为直径的圆上时,直线l的方程为y=±![]() (x-2).
(x-2).


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源:2013届北京四中高二上学期期中考试数学 题型:解答题
已知O为坐标原点,△AOB中,边OA所在的直线方程是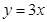 ,边AB所在的直
,边AB所在的直
线方程是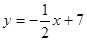 ,且顶点B的横坐标为6。
,且顶点B的横坐标为6。
(1)求△AOB中,与边AB平行的中位线所在直线的方程;
(2)求△AOB的面积;
(3)已知OB上有点D,满足△AOD与△ABD的面积比为2,求AD所在的直线方程。
查看答案和解析>>
科目:高中数学 来源:2010年江西省高三上学期开学模拟考试文科数学卷 题型:选择题
平面直向坐标系中,O为坐标原点,已知两点A(3,1) B(-1,3)若点C满足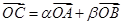 ,其中
,其中
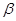 ∈R且
∈R且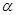 +
+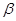 =1,则点C的轨迹方程为
。
=1,则点C的轨迹方程为
。
A.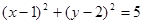 B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
查看答案和解析>>
科目:高中数学 来源: 题型:
平面直向坐标系中,O为坐标原点,已知两点A(3,1) B(-1,3)若点C满足![]() ,其中
,其中![]()
![]() ∈R且
∈R且![]() +
+![]() =1,则点C的轨迹方程为 。
=1,则点C的轨迹方程为 。
A.![]() B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com