
(本题满分12)
如图,在三棱锥S-ABC中,ΔABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=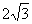 ,M,N分别为AB,SB的中点。
,M,N分别为AB,SB的中点。
(Ⅰ)求异面直线AC与SB所成角; (Ⅱ)求二面角 N-CM-B的大小;
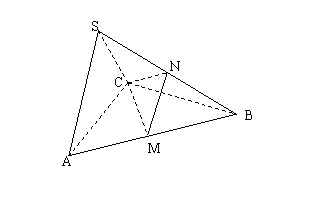 (Ⅲ)求点B到平面CMN的距离。
(Ⅲ)求点B到平面CMN的距离。
解:
(I)取AC 中点D,连结SD,DB。
因为SA=SC,AB=BC,所以AC⊥SD且AC⊥BD,所以AC⊥平面SDB.
又SB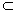 平面SDB,所以AC⊥SB.所以异面直线AC与SB所成角为90
平面SDB,所以AC⊥SB.所以异面直线AC与SB所成角为90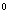 。…………4分
。…………4分
(II)因为AC⊥平面SDB,AC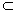 平面ABC, 所以平面SDC⊥平面ABC.
平面ABC, 所以平面SDC⊥平面ABC.
过N作NE⊥BD于E,则NE⊥平面ABC,
过E作EF⊥CM于F,连结NF,则NF⊥CM,
所以∠NFE为二面角N-CM-B的平面角。
因为平面SAC⊥平面ABC, SD⊥AC,所以SD⊥平面ABC.
又因为NE⊥平面ABC,所以NE∥SD。
由于SN=NB,所以NE=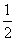 SD=
SD=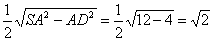 ,且ED=EB.
,且ED=EB.
在正△ABC中,由平面几何知识可求得EF=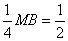 .
.
在Rt△NEF中,tan∠NFE=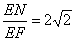
所以二面角N-CM-B的大小是arctan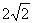 .
………………………………8分
.
………………………………8分
(III)在Rt△NEF中,NF=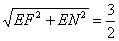 ,所以
,所以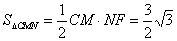 ,
,
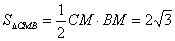 .
.
设点B到平面CMN的距离为h,
因为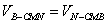 ,NE⊥平面CMB,
,NE⊥平面CMB,
所以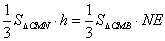 则h=
则h=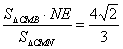
即点B到平面CMN的距离为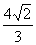 。
………………………………12分
。
………………………………12分


科目:高中数学 来源:2015届吉林省高一上学期期末考试文科数学试卷(解析版) 题型:解答题
(本题满分12分)如图所示,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.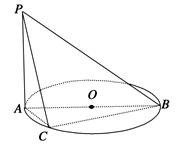
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三上学期期中理科数学试卷(解析版) 题型:解答题
(本题满分12分)
如图,甲船以每小时30 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省营口市高一上学期期末检测数学试卷 题型:解答题
.(本题满分12分)
如图所示, ⊥矩形
⊥矩形 所在的平面,
所在的平面, 分别是
分别是 、
、 的中点,
的中点,

(1)求证: ∥平面
∥平面 ;
;
(2)求证: ⊥
⊥ ;
;
(3)若 ,求证:平面
,求证:平面 ⊥平面
⊥平面 .
.
查看答案和解析>>
科目:高中数学 来源:2010年山西省忻州市高二下学期期末联考(文科)数学卷 题型:解答题
(本题满分12分)
如图所示,已知 M、N分别是
M、N分别是
AC、AD的中点,BC CD.
CD.
(1)求证:MN∥平面BCD;
(2)求证:平面ACD 平面ABC;
平面ABC;
(3)若AB=1,BC= ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.

查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省高二上学期期末考试数学理卷 题型:解答题
.(本题满分12分)
如图,四棱锥 的底面
的底面 是正方形,侧面
是正方形,侧面
 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面, ,
,
 ,
, 、
、 分别是
分别是 、
、 的中点。
的中点。
(1)求证: ;
;
(2)求二面角 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com