
【题目】已知![]() ,函数
,函数![]() .
.
(1)若![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
(2)若![]() 是
是![]() 的极小值点,求
的极小值点,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)将![]() 代入函数
代入函数![]() 的解析式,得出
的解析式,得出![]() ,构造函数
,构造函数![]() ,利用导数求出函数
,利用导数求出函数![]() 的最大值为
的最大值为![]() ,从而可证明出所证不等式成立;
,从而可证明出所证不等式成立;
(2)分![]() 、
、![]() 和
和![]() 三种情况讨论,分析函数
三种情况讨论,分析函数![]() 的导函数
的导函数![]() 在
在![]() 附近符号的变化,结合条件“
附近符号的变化,结合条件“![]() 是
是![]() 的极小值点”,可得出实数
的极小值点”,可得出实数![]() 的取值范围.
的取值范围.
(1)若![]() ,
,![]() .
.
设函数![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以在![]() 上,
上,![]() .
.
又因为当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() ;
;
(2)(i)若![]() ,由(1)可知当
,由(1)可知当![]() 时,
时,![]() ,这与
,这与![]() 是
是![]() 的极小值点矛盾.
的极小值点矛盾.
(ii)若![]() ,对于方程
,对于方程![]() ,因为
,因为![]() ,且
,且![]() ,
,
故方程有两个实根![]() 、
、![]() ,且满足
,且满足![]() .
.
当![]() 时,
时,![]() ,
,
结合(1),可得![]() .
.
这与![]() 是
是![]() 的极小值点矛盾.
的极小值点矛盾.
(iii)若![]() ,设函数
,设函数![]() .
.
由于当![]() 时,
时,![]() ,故
,故![]() 与
与![]() 符号相同.
符号相同.
又![]() ,所以
,所以![]() 是
是![]() 的极小值点等价于
的极小值点等价于![]() 是
是![]() 的极小值点.
的极小值点.
![]() .
.
由![]() 得,
得,![]() 或
或![]() .
.
如果![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 且
且![]() 时,
时,![]() ,所以
,所以![]() 不是
不是![]() 的极小值点.
的极小值点.
如果![]() ,则当
,则当![]() 时,
时,![]() ,所以
,所以![]() 不是
不是![]() 的极小值点.
的极小值点.
如果![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 是
是![]() 的极小值点,从而
的极小值点,从而![]() 是
是![]() 的极小值点,此时
的极小值点,此时![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
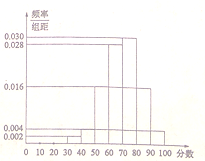
【题目】2016年某市政府出台了“2020年创建全国文明城市(简称创文)”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:①调查对象为本市市民,被调查者各自独立评分;②采用百分制评分, ![]() 内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
(1)求被调查者满意或非常满意该项目的频率;
(2)若从该市的全体市民中随机抽取3人,试估计恰有2人非常满意该项目的概率;
(3)已知在评分低于60分的被调查者中,老年人占![]() ,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记
,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记![]() 为群众督查员中老年人的人数,求随机变量
为群众督查员中老年人的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一个动点M到定点F(3,0)的距离和它到定直线l:x=6的距离之比是常数![]() .
.
(1)求动点M的轨迹T的方程;
(2)若直线l:x+y-3=0与轨迹T交于A,B两点,且线段AB的垂直平分线与T交于C,D两点,试问A,B,C,D是否在同一个圆上?若是,求出该圆的方程;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 是曲线
是曲线![]() :
:![]() 上的一个动点,曲线
上的一个动点,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 是坐标原点,①
是坐标原点,①![]() ;②
;②![]() 的面积为定值;③曲线
的面积为定值;③曲线![]() 上存在两点
上存在两点![]() ,
,![]() 使得
使得![]() 是等边三角形;④曲线
是等边三角形;④曲线![]() 上存在两点
上存在两点![]() ,
,![]() 使得
使得![]() 是等腰直角三角形,其中真命题的个数是( )
是等腰直角三角形,其中真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点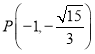 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,使得
两点,使得![]() ?若存在,求出直线的方程;若不存在,说明理由.
?若存在,求出直线的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学成就甚大,在世界科技史上占有重要的地位.“算经十书”是汉、唐千余年间陆续出现的10部数学著作,包括《周髀算经》、《九章算术》、……、《缀术》等,它们曾经是隋唐时期国子监算学科的教科书.某中学图书馆全部收藏了这10部著作,其中4部是古汉语本,6部是现代译本,若某学生要从中选择2部作为课外读物,至少有一部是现代译本的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推,若该数列前
,依此类推,若该数列前![]() 项和
项和![]() 满足:①
满足:①![]() ②
②![]() 是2的整数次幂,则满足条件的最小的
是2的整数次幂,则满足条件的最小的![]() 为
为
A. 21B. 91C. 95D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,设
,设![]() ,
,![]() 是椭圆
是椭圆![]() 的两个短轴端点,
的两个短轴端点,![]() 是椭圆
是椭圆![]() 的长轴左端点.
的长轴左端点.
(1)当![]() 时,设点
时,设点![]() ,
,![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,且直线
,且直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,若经过
时,若经过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,求
为坐标原点,求![]() 与
与![]() 的面积之差的最大值.
的面积之差的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com