
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,
,![]() .
.
(1)若![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】天气预报说,今后三天每天下雨的概率相同,现用随机模拟的方法预测三天中有两天下雨的概率,用骰子点数来产生随机数.依据每天下雨的概率,可规定投一次骰子出现1点和2点代表下雨;投三次骰子代表三天;产生的三个随机数作为一组.得到的10组随机数如下:613,265,114,236,561,435,443,251,154,353.则在此次随机模拟试验中,每天下雨的概率的近似值是__________,三天中有两天下雨的概率的近似值为__________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一旅游区有两个新建项目![]() 、
、![]() .
.![]() 项目的一期投资额
项目的一期投资额![]() 与利润
与利润![]() 近似满足
近似满足![]() .
.![]() 项目的一期投资额
项目的一期投资额![]() 与利润
与利润![]() 的关系如散点图所示,其中
的关系如散点图所示,其中![]()
![]() ,
,![]() ,
,![]() .一商家欲向这两个项目一期随机投资,其中投资
.一商家欲向这两个项目一期随机投资,其中投资![]() 项目不超过10(本题未注明金额单位的,单位均为百万元).投资
项目不超过10(本题未注明金额单位的,单位均为百万元).投资![]() 、
、![]() 相互独立.
相互独立.
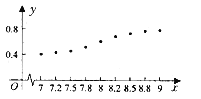
(1)用最小二乘法求![]() 与
与![]() 的回归直线方程;
的回归直线方程;
(2)商家投资![]() 项目的概率是0.4,投资
项目的概率是0.4,投资![]() 项目的概率是0.6.设商家这次投资获得的利润最大值为
项目的概率是0.6.设商家这次投资获得的利润最大值为![]() ,利用(1)的结果,求
,利用(1)的结果,求![]() .
.
附参考公式: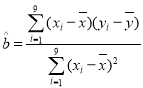 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]()
![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数字期望)
的分布列和均值(数字期望)![]() ;
;
(3)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年9月第三周是国家网络安全宣传周.某学校为调查本校学生对网络安全知识的了解情况,组织了《网络信息辨析测试》活动,并随机抽取50人的测试成绩绘制了频率分布直方图如图所示:

(1)某学生的测试成绩是75分,你觉得该同学的测试成绩低不低?说明理由;
(2)将成绩在![]() 内定义为“合格”;成绩在
内定义为“合格”;成绩在![]() 内定义为“不合格”.①请将下面的
内定义为“不合格”.①请将下面的![]() 列联表补充完整; ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由;
列联表补充完整; ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由;
合格 | 不合格 | 合计 | |
男生 | 26 | ||
女生 | 6 | ||
合计 |
(3)在(2)的前提下,对50人按是否合格,利用分层抽样的方法抽取5人,再从5人中随机抽取2人,求恰好2人都合格的概率.附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.65 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查“双11”消费活动情况,某校统计小组分别走访了![]() 、
、![]() 两个小区各20户家庭,他们当日的消费额按
两个小区各20户家庭,他们当日的消费额按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,分别用频率分布直方图与茎叶图统计如下(单位:元):
分组,分别用频率分布直方图与茎叶图统计如下(单位:元):
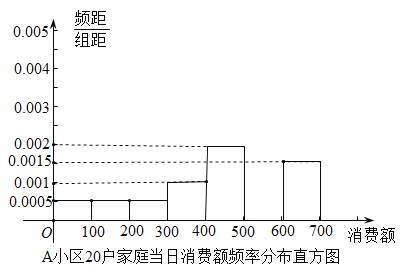
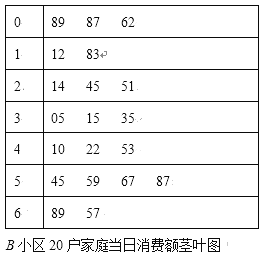
(1)分别计算两个小区这20户家庭当日消费额在![]() 的频率,并补全频率分布直方图;
的频率,并补全频率分布直方图;
(2)分别从两个小区随机选取1户家庭,求这两户家庭当日消费额在![]() 的户数为1时的概率(频率当作概率使用);
的户数为1时的概率(频率当作概率使用);
(3)运用所学统计知识分析比较两个小区的当日网购消费水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若点![]() 为点
为点![]() 在平面
在平面![]() 上的正投影,则记
上的正投影,则记![]() .如图,在棱长为1的正方体
.如图,在棱长为1的正方体![]() 中,记平面
中,记平面![]() 为
为![]() ,平面
,平面![]() 为
为![]() ,点
,点![]() 是线段
是线段![]() 上一动点,
上一动点,![]() .给出下列四个结论:
.给出下列四个结论:
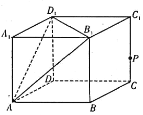
①![]() 为
为![]() 的重心;
的重心;
②![]() ;
;
③当![]() 时,
时,![]() 平面
平面![]() ;
;
④当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() .
.
其中,所有正确结论的序号是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下几个结论:
①命题![]() ,
,![]() ,则
,则![]() ,
,![]()
②命题“若![]() ,则
,则![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() ,则
,则![]() ”
”
③“命题![]() 为真”是“命题
为真”是“命题![]() 为真”的充分不必要条件
为真”的充分不必要条件
④若![]() ,则
,则![]() 的最小值为4
的最小值为4
其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com