
分析 (1)点P在曲线C上,Q在直线l上,若$α=\frac{3}{4}π$,利用|PQ|的最小值为圆心到直线的距离减去半径,即可求线段|PQ|的最小值;
(2)设直线l与曲线C有两个不同的交点,当圆心到直线的距离等于半径时,即$\frac{|2-2k|}{{\sqrt{{k^2}+1}}}=\sqrt{2}$,即可求直线l的斜率k的范围.
解答 解:(1)$α=\frac{3}{4}π$时,易知直线l的方程为x+y-4=0,…(2分)
曲线C:$ρ=\sqrt{2}$的普通方程为x2+y2=2.…(3分)
由题意知|PQ|的最小值为圆心到直线的距离减去半径,
所以$|PQ{|_{min}}=\frac{|0+0-4|}{{\sqrt{{1^2}+{1^2}}}}-\sqrt{2}=2\sqrt{2}-\sqrt{2}=\sqrt{2}$.…(5分)
(2)因为α=90°时,直线l与C没有交点,
所以直线l可化为普通方程为y-2=tanα(x-2),…(7分)
令k=tanα,即kx-y+2-2k=0,
当圆心到直线的距离等于半径时,即$\frac{|2-2k|}{{\sqrt{{k^2}+1}}}=\sqrt{2}$,
解得$k=2±\sqrt{3}$,此时它们相切,…(9分)
所以$k∈(2-\sqrt{3},\;\;2+\sqrt{3})$.…(10分)
点评 本题考查直线与圆的位置关系,考查参数方程、极坐标方程、直角坐标方程的互化,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{3}$x | C. | y=±$\frac{1}{3}$x | D. | y=±3x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直角三角形ABC中,∠B=90°,$AB=\frac{1}{2}AC=1$,点M,N分别在边AB和AC上(M点和B点不重合),将△AMN沿MN翻折,△AMN变为△A'MN,使顶点A'落在边BC上(A'点和B点不重合).设∠ANM=θ
如图,在直角三角形ABC中,∠B=90°,$AB=\frac{1}{2}AC=1$,点M,N分别在边AB和AC上(M点和B点不重合),将△AMN沿MN翻折,△AMN变为△A'MN,使顶点A'落在边BC上(A'点和B点不重合).设∠ANM=θ查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | -12 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线$x=\frac{π}{4}$对称 | B. | 关于直线$x=-\frac{π}{4}$对称 | ||
| C. | 关于直线$x=\frac{π}{2}$对称 | D. | 关于直线$x=-\frac{π}{2}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1x2<0 | B. | 0<x1x2<1 | C. | x1x2=1 | D. | x1x2>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
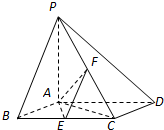 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com