
【题目】在平面直角坐标系中,已知点![]() 与两个定点
与两个定点![]() ,
,![]() 的距离之比为
的距离之比为![]() .
.
(1)求点![]() 的坐标所满足的关系式;
的坐标所满足的关系式;
(2)求![]() 面积的最大值;
面积的最大值;
(3)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)3;(3)
(2)3;(3)![]()
【解析】
(1)根据题意,结合两点间距离公式,可以得到等式,化简后得到点![]() 的坐标所满足的关系式;
的坐标所满足的关系式;
(2)设![]() 是曲线上任一点,求出
是曲线上任一点,求出![]() 的表达式,结合
的表达式,结合![]() 的取值范围,可以求出
的取值范围,可以求出![]() 面积的最大值;
面积的最大值;
(3)![]() 恒成立,则
恒成立,则![]() 恒成立. 设
恒成立. 设![]() ,当它与圆
,当它与圆![]() 相切时,
相切时,![]() 取得最大和最小值,利用点到直线距离公式,可以求出
取得最大和最小值,利用点到直线距离公式,可以求出![]() 取得最大和最小值,最后可以求出实数
取得最大和最小值,最后可以求出实数![]() 的取值范围.
的取值范围.
(1)设![]() 的坐标是
的坐标是![]() ,由
,由![]() ,得
,得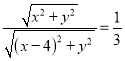 ,
,
化简得![]() .
.
(2)由(1)得![]() ,点
,点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上.
为半径的圆上.
设![]() 是曲线上任一点,则
是曲线上任一点,则![]() ,
,
又![]() ,故
,故![]() 的最大值为:
的最大值为:![]() .
.
(3)由(1)得:圆的方程是![]()
若![]() 恒成立,则
恒成立,则![]() 恒成立.
恒成立.
设![]() ,当它与圆
,当它与圆![]() 相切时,
相切时,
![]() 取得最大和最小值,
取得最大和最小值,
由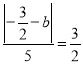 得:
得:![]() ,
,![]() ,
,
故当![]() 时,原不等式恒成立.
时,原不等式恒成立.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图像相邻的两个对称中心之间的距离为
,其图像相邻的两个对称中心之间的距离为![]() ,且有一条对称轴为直线
,且有一条对称轴为直线![]() ,则下列判断正确的是 ( )
,则下列判断正确的是 ( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
D. 函数![]() 的图像关于点
的图像关于点![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了
市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
不支持 | 支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否有![]() 的把握认为支持申办足球世界杯与性别有关;
的把握认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退体老人中随机抽取
位退体老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了![]() 位医护人员的关爱患者考核分数(患者考核:
位医护人员的关爱患者考核分数(患者考核:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:
表示;医护专业知识考核分数(试卷考试:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到
的线性回归方程(计算结果精确到![]() );
);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计当某医护人员的医护专业知识考核分数为![]() 分时,他的关爱患者考核分数(精确到
分时,他的关爱患者考核分数(精确到![]() ).
).
参考公式及数据:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名的![]() 周髀算经
周髀算经![]() 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷![]() 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸![]() 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为![]() 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分![]() 则“立春”时日影长度为
则“立春”时日影长度为![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ex﹣ax2﹣2x+b(e为自然对数的底数,a,b∈R).
(Ⅰ)设f′(x)为f(x)的导函数,证明:当a>0时,f′(x)的最小值小于0;
(Ⅱ)若a<0,f(x)>0恒成立,求符合条件的最小整数b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示. 
(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com