
【题目】如图,在矩形![]() 中,AB=2AD,
中,AB=2AD,![]() 为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
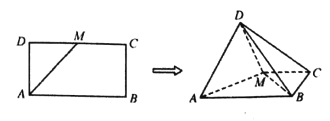
(1)当AB=2时,求三棱锥![]() 的体积;
的体积;
(2)求证:BM⊥AD.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)取AM的中点N,连接DN,易证得DN⊥平面ABCM,由![]() ,只需计算
,只需计算![]() 和
和![]() 即可;
即可;
(2)可证BM⊥DN和BM⊥AM,从而证得BM⊥平面ADM,从而得证.
试题解析:
(1)取AM的中点N,连接DN.

∵在矩形![]() 中,
中,![]() 为DC的中点,AB=2AD,∴DM=AD.
为DC的中点,AB=2AD,∴DM=AD.
又N为AM的中点,∴DN⊥AM.
又∵平面ADM⊥平面ABCM,平面![]() ,
,![]() 平面ADM,
平面ADM,
∴DN⊥平面ABCM.
∵AD=1,∴![]() .
.
又![]() ,∴
,∴![]() .
.
证明:(2)由(1)可知,DN⊥平面ABCM.
又![]() 平面ABCM,∴BM⊥DN.
平面ABCM,∴BM⊥DN.
在矩形![]() 中,AB=2AD,M为MC中点,
中,AB=2AD,M为MC中点,
∴△ADM,△BCM都是等腰直角三角形,且∠ADM=90°,∠BCM=90°,∴BM⊥AM.
又DN,![]() 平面ADM,
平面ADM,![]() ,∴BM⊥平面ADM.
,∴BM⊥平面ADM.
又![]() 平面ADM,∴BM⊥AD.
平面ADM,∴BM⊥AD.


科目:高中数学 来源: 题型:
【题目】椭圆![]() ,其中
,其中![]() ,焦距为2,过点
,焦距为2,过点![]() 的直线l与椭圆C交于点A,B,点B在A,M之间.又线段AB的中点的横坐标为
的直线l与椭圆C交于点A,B,点B在A,M之间.又线段AB的中点的横坐标为![]() ,且
,且![]() .
.
(1)求椭圆C的标准方程.
(2)求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.

(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
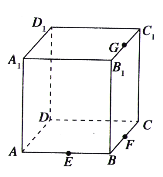
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;②点![]() 在直线
在直线![]() 上运动时,总有
上运动时,总有![]() ;③点
;③点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积的定值;④若点
的体积的定值;④若点![]() 是正方体的面
是正方体的面![]() 内的一动点,且
内的一动点,且![]() 到点
到点![]() 和
和![]() 距离相等,则点
距离相等,则点![]() 的轨迹是一条线段.
的轨迹是一条线段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() ,(
,(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的普通方程;
的普通方程;
(2)若![]() 分别为曲线
分别为曲线![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某超市的一种商品在过去的一个月内(以30天计算),销售价格![]() 与时间(天)的函数关系近似满足
与时间(天)的函数关系近似满足![]() ,销售量
,销售量![]() 与时间(天)的函数关系近似满足
与时间(天)的函数关系近似满足 .
.
(1)试写出该商品日销售金额![]() 关于时间
关于时间![]() 的函数表达式;
的函数表达式;
(2)求该商品的日销售金额![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红铃虫的产卵数y和温度x有关,现收集了6组观测数据于下表中,通过散点图可以看出样本点分布在一条指数型函数y=![]() 的图象的周围.
的图象的周围.
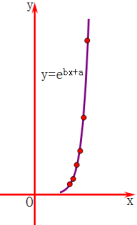
(1)试求出y关于x的上述指数型的回归曲线方程(结果保留两位小数);
(2)试用(1)中的回归曲线方程求相应于点(24,17)的残差![]() .(结果保留两位小数)
.(结果保留两位小数)
温度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
产卵数y(个) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
几点说明:
①结果中的![]() 都应按题目要求保留两位小数.但在求
都应按题目要求保留两位小数.但在求![]() 时请将
时请将![]() 的值多保留一位即用保留三位小数的结果代入.
的值多保留一位即用保留三位小数的结果代入.
②计算过程中可能会用到下面的公式:回归直线方程的斜率![]() =
= =
= ,截距
,截距![]() .
.
③下面的参考数据可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com