
【题目】已知O为坐标原点,向量 ![]() =(sinα,1),
=(sinα,1), ![]() =(cosα,0),
=(cosα,0), ![]() =(﹣sinα,2),点P是直线AB上的一点,且
=(﹣sinα,2),点P是直线AB上的一点,且 ![]() =
= ![]() .
.
(1)若O,P,C三点共线,求tanα的值;
(2)在(Ⅰ)条件下,求 ![]() +sin2α的值.
+sin2α的值.
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面是正方形,每条侧棱的长都是底面边长的 ![]() 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点. 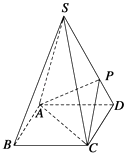
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P﹣AC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程 ![]() =﹣1表示的曲线即为函数y=f(x),有如下结论:( ) ①函数f(x)在R上单调递减;
=﹣1表示的曲线即为函数y=f(x),有如下结论:( ) ①函数f(x)在R上单调递减;
②函数F(x)=4f(x)+3x不存在零点;
③函数y=f(x)的值域是R;
④若函数g(x)和f(x)的图象关于原点对称,则函数y=g(x)的图象就是方程 ![]() =﹣1确定的曲线.
=﹣1确定的曲线.
其中所有正确的命题序号是( )
A.①②
B.②③
C.①③④
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
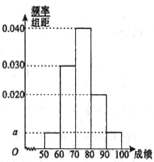
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(2x+ ![]() )+tan
)+tan ![]() cos2x.
cos2x.
(1)求f(x)的最小正周期及其图象的对称轴方程;
(2)求函数f(x)在区间(0, ![]() )上的值域.
)上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin ωxcos ωx-sin2ωx+1(ω>0)图象的相邻两条对称轴之间的距离为
sin ωxcos ωx-sin2ωx+1(ω>0)图象的相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求ω的值及函数f(x)的单调递减区间;
(Ⅱ)如图,在锐角三角形ABC中有f(B)=1,若在线段BC上存在一点D使得AD=2,且AC=![]() ,CD=
,CD=![]() -1,求三角形ABC的面积.
-1,求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() 的参数方程为
的参数方程为  ,曲线
,曲线 ![]() 的参数方程为
的参数方程为 ![]() ,设直线
,设直线 ![]() 与曲线
与曲线 ![]() 交于两点
交于两点 ![]() ,
,
(1)求 ![]() ;
;
(2)设 ![]() 为曲线
为曲线 ![]() 上的一点,当
上的一点,当 ![]() 的面积取最大值时,求点
的面积取最大值时,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线 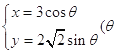 为参数)和定点
为参数)和定点 ![]() F1 , F2是圆锥曲线的左右焦点。
F1 , F2是圆锥曲线的左右焦点。
(1)求经过点F2且垂直于直线AF1的直线l的参数方程;
(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com