
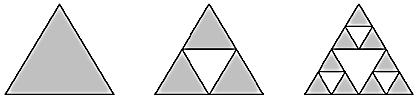
【题目】谢尔宾斯基三角形(Sierpinskitriangle)是由波兰数学家谢尔宾斯基在1915年提出的,如图先作一个三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色三角形代表挖去的面积,那么灰色三角形为剩下的面积(我们称灰色部分为谢尔宾斯基三角形).若通过该种方法把一个三角形挖3次,然后在原三角形内部随机取一点,则该点取自谢尔宾斯基三角形的概率为______.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 、
、![]() 的值;
的值;
(2)设函数![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
①当![]() 时,求
时,求![]() 的最大值;
的最大值;
②若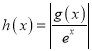 是单调递减函数,求实数
是单调递减函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若规定问卷得分不低于70分的市民称为“环保关注者”,请完成答题卡中的![]() 列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.视频率为概率.
①在我市所有“环保达人”中,随机抽取3人,求抽取的3人中,既有男“环保达人”又有女“环保达人”的概率;
②为了鼓励市民关注环保,针对此次的调查制定了如下奖励方案:“环保达人”获得两次抽奖活动;其他参与的市民获得一次抽奖活动.每次抽奖获得红包的金额和对应的概率.如下表:
红包金额(单位:元) | 10 | 20 |
概率 |
|
|
现某市民要参加此次问卷调查,记![]() (单位:元)为该市民参加间卷调查获得的红包金额,求
(单位:元)为该市民参加间卷调查获得的红包金额,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日,庆祝中华人民共和国成立70周年大会、阅兵式、群众游行在北京隆重举行,这次阅兵编59个方(梯)队和联合军乐团,总规模约1.5万人,各型飞机160余架、装备580余套,是近几次阅兵中规模最大的一次.某机构统计了观看此次阅兵的年龄在30岁至80岁之间的100个观众,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求![]() 的值及这100个人的平均年龄(同一组中的数据用该组区间的中点值为代表);
的值及这100个人的平均年龄(同一组中的数据用该组区间的中点值为代表);
(2)用分层抽样的方法在年龄为![]() 、
、![]() 的人中抽取5人,再从抽取的5人中随机抽取2人接受采访,求接受采访的2人中年龄在
的人中抽取5人,再从抽取的5人中随机抽取2人接受采访,求接受采访的2人中年龄在![]() 的恰有1人的概率.
的恰有1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家商场销售一种商品,该商品一天的需求量在![]() 范围内等可能取值,该商品的进货量也在
范围内等可能取值,该商品的进货量也在![]() 范围内取值(每天进货1次).这家商场每销售一件该商品可获利60元;若供不应求,可从其他商店调拨,销售一件该商品可获利40元;若供大于求,剩余的每处理一件该商品亏损20元.设该商品每天的需求量为
范围内取值(每天进货1次).这家商场每销售一件该商品可获利60元;若供不应求,可从其他商店调拨,销售一件该商品可获利40元;若供大于求,剩余的每处理一件该商品亏损20元.设该商品每天的需求量为![]() ,每天的进货量为
,每天的进货量为![]() 件,该商场销售该商品的日利润为
件,该商场销售该商品的日利润为![]() 元.
元.
(1)写出这家商场销售该商品的日利润为![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)写出供大于求,销售![]() 件商品时,日利润
件商品时,日利润![]() 的分布列;
的分布列;
(3)当进货量![]() 多大时,该商场销售该商品的日利润的期望值最大?并求出日利润的期望值的最大值.
多大时,该商场销售该商品的日利润的期望值最大?并求出日利润的期望值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD![]() A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线( )
A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线( )
A.不存在B.有且只有两条C.有且只有三条D.有无数条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com