
 为了了解一种植物果实的情况,随机抽取一批该植物果实样本测量重量(单位:克),按照[27.5,32.5),[32.5,37.5),[37.5,42.5),[42.5,47.5),[47.5,52.5]分为5组,其频率分布直方图如图所示.
为了了解一种植物果实的情况,随机抽取一批该植物果实样本测量重量(单位:克),按照[27.5,32.5),[32.5,37.5),[37.5,42.5),[42.5,47.5),[47.5,52.5]分为5组,其频率分布直方图如图所示.分析 (1)利用频率和为1,求图中a的值;
(2)用该组区间的中点值作代表,估计这种植物果实重量的平均数$\overline{x}$和方差s2;
(3)利用古典概型的概率公式求解即可.
解答 解:(1)由题意,(0.015+0.020+0.040+a+0.075)×5=1,∴a=0.05;
(2)平均数$\overline{x}$=(30×0.02+35×0.04+40×0.075+45×0.05+50×0.015)×5=40,
S2=(30-40)2×0.1+(35-40)2×0.2+(40-40)2×0.375+(45-40)2×0.25+(50-40)2×0.075=28.75,
(3)40×0.1=4,40×0.075=3,
随机抽取2个,有${C}_{7}^{2}$=21种情况,都抽到优质果实的概率1-$\frac{{C}_{4}^{2}}{21}$=$\frac{5}{7}$.
点评 本题考查频率分布直方图,考查概率的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
各项为正的等比数列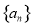 中,
中,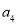 与
与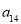 的等比中项为
的等比中项为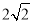 ,则
,则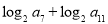 的值为( )
的值为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3\sqrt{3}}{2}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{3\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{8}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两条相交直线 | B. | 两条射线 | C. | 一条直线 | D. | 一条射线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com