
【题目】已知椭圆![]() 的离心率e=
的离心率e=![]() ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设直线![]() 过椭圆的左端点A,与椭圆的另一个交点为B.,AB的垂直平分线交
过椭圆的左端点A,与椭圆的另一个交点为B.,AB的垂直平分线交![]() 轴于点
轴于点![]() ,且
,且![]() ·
·![]() =4,求
=4,求![]() 的值.
的值.
【答案】(1) ![]() (2)y0=±2
(2)y0=±2![]() 或y0=±
或y0=±![]() .
.
【解析】试题分析:1)由离心率求得a和c的关系,进而根据c2=a2﹣b2求得a和b的关系,进而根据菱形的面积公式,求得a和b,则椭圆的方程可得.
(2)由(1)可求得A点的坐标,设出点B的坐标和直线l的斜率,表示出直线l的方程与椭圆方程联立,消去y,由韦达定理求得点B的横坐标的表达式,进而利用直线方程求得其纵坐标表达式,表示出|AB|进而求得k,则直线的斜率可得.设线段AB的中点为M,当k=0时点B的坐标是(2,0),线段AB的垂直平分线为y轴,进而根据![]() ,求得y0;当k≠0时,可表示出线段AB的垂直平分线方程,令x=0得到y0的表达式根据
,求得y0;当k≠0时,可表示出线段AB的垂直平分线方程,令x=0得到y0的表达式根据![]() ,,求得y0.
,,求得y0.
试题解析:
(1)由e=![]() =
=![]() ,得3a2=4c2.再由c2=a2-b2,得a=2b.
,得3a2=4c2.再由c2=a2-b2,得a=2b.
由题意可知![]() ×2a×2b=4,即ab=2.解方程组
×2a×2b=4,即ab=2.解方程组![]() 得a=2,b=1.
得a=2,b=1.
所以椭圆的方程为![]() .
.
(2)由(1)可知A(-2,0).设B点的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程
的方程![]() .于是A,B两点的坐标满足方程组
.于是A,B两点的坐标满足方程组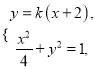
由方程组消去y并整理,得![]() .
.
由![]() ,得
,得![]() .从而
.从而![]() .
.
设线段AB的中点为M,则M的坐标为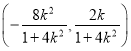 .
.
以下分两种情况:
①当k=0时,点B的坐标为(2,0),线段AB的垂直平分线为y轴,于是![]() =(-2,-y0),
=(-2,-y0),
![]() =(2,-y0).由
=(2,-y0).由![]() ·
·![]() =4,得y0=±2
=4,得y0=±2![]() .
.
②当k≠0时,线段AB的垂直平分线方程为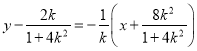 .
.
令x=0,解得![]() ,
,
由![]() =(-2,-y0),
=(-2,-y0), ![]() =(x1,y1-y0).
=(x1,y1-y0).
![]() ·
·![]() =-2x1-y0(y1-y0)
=-2x1-y0(y1-y0)
=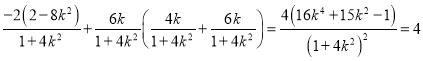 ,
,
整理得7k2=2,故k=±![]() .所以y0=±
.所以y0=±![]() .综上,y0=±2
.综上,y0=±2![]() 或y0=±
或y0=±![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]()
(1)设![]() ,
,![]() ,若函数
,若函数![]() 存在零点,求a的取值范围;
存在零点,求a的取值范围;
(2)若![]() 是偶函数,求
是偶函数,求![]() 的值;
的值;
(3)在(2)条件下,设![]() ,若函数
,若函数![]() 与
与![]() 的图象只有一个公共点,求实数b的取值范围.
的图象只有一个公共点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. (Ⅰ)求证:AD⊥平面BFED;
(Ⅱ)在线段EF上是否存在一点P,使得平面PAB与平面ADE所成的锐二面角的余弦值为 ![]() .若存在,求出点P的位置;若不存在,说明理由.
.若存在,求出点P的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,点(a,b)在4xcosB﹣ycosC=ccosB上.
(1)cosB的值;
(2)若 ![]()
![]() =3,b=3
=3,b=3 ![]() ,求a和c.
,求a和c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B均为锐角,则cosA>sinB是△ABC为钝角三角形的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x2)+ax.(a≤0)
(1)若f(x)在x=0处取得极值,求a的值;
(2)讨论f(x)的单调性;
(3)证明:(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<
)< ![]() (n∈N* , e为自然对数的底数).
(n∈N* , e为自然对数的底数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com