
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)讨论![]() 和
和![]() 是函数
是函数![]() 的极大值还是极小值;
的极大值还是极小值;
(2)过点![]() 作曲线
作曲线![]() 的切线,求此切线方程.
的切线,求此切线方程.
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 是直线
是直线![]() 上的一动点,过点
上的一动点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
(1)当切线![]() 的长度为
的长度为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)若![]() 的外接圆为圆
的外接圆为圆![]() ,试问:当
,试问:当![]() 在直线
在直线![]() 上运动时,圆
上运动时,圆![]() 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
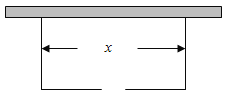
【题目】围建一个面积为360![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元)
(单位:元)
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有学生 ![]() 人,其中一年级
人,其中一年级 ![]() 人,二、三年级各
人,二、三年级各 ![]() 人,现要用抽样方法抽取
人,现要用抽样方法抽取 ![]() 人形成样本,将学生按一、二、三年级依次统一编号为
人形成样本,将学生按一、二、三年级依次统一编号为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,如果抽得号码有下列四种情况:
,如果抽得号码有下列四种情况:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
②![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
③![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
④![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
其中可能是由分层抽样得到,而不可能是由系统抽样得到的一组号码为 ![]()
A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com