某厂预计从2008年初开始的前n个月内,市场对某种产品的需求总量f(n)与月份n的近似关系为:f(n)=n(n+1)(35-2n),(单位:台),n∈N*,且n≤12
(1)写出2008年第n个月的需求量g(n)与月份n的关系式
(2)如果该厂此种产品每月生产a台,为保证每月满足市场需求,则a至少应为多少?
【答案】
分析:(1)把x=1代入到f(x)得到f(1)即为g(1),当x≥2时,g(x)=f(x)-f(x-1)化简得出解析式并求出当x为多少时g(x)的最大值即可;
(2)对一切x∈{1,2,,12}有px≥f(x)列出不等式得到P≥一个函数,求出函数的最大值得到P的取值范围.
解答:解:(1)g(1)=f(1)=1×2×33=66,
g(n)=f(n)-f(n-1)
=n(n+1)(35-2n)-[(n-1)n(35-2(n-1)],
=-6n
2+72n.
当n=1时,=-6n
2+72n=66=g(1).
∴g(n)=-6n
2+72n.
(2)依题意,对一切n∈{1,2,,12}有an≥f(n).
∴a≥(n+1)(35-2n),n∈{1,2,,12}.
设
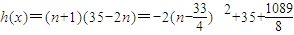
,
∴h(x)
max=h(8)=171.故a≥171.
故保证每月满足市场需求,则a至少应为171台.
点评:考查学生根据实际问题选择函数类型的能力.理解函数最值及其意义.

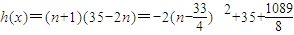 ,
,

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案