
【题目】设数列{an}的前项和为Sn , 且Sn= ![]() ,{bn}为等差数列,且a1=b1 , a2(b2﹣b1)=a1 .
,{bn}为等差数列,且a1=b1 , a2(b2﹣b1)=a1 .
(1)求数列{an}和{bn}通项公式;
(2)设 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
【答案】
(1)解:当n=1时,a1=S1=1,
当n≥2时,an=Sn﹣Sn﹣1=( ![]() )﹣(
)﹣( ![]() )=
)= ![]() ,
,
经验证当n=1时,此式也成立,所以 ![]() ,从而b1=a1=1,
,从而b1=a1=1, ![]() ,
,
又因为{bn}为等差数列,所以公差d=2,∴bn=1+(n﹣1)2=2n﹣1,
故数列{an}和{bn}通项公式分别为: ![]() ,bn=2n﹣1.
,bn=2n﹣1.
(2)解:由(1)可知 ![]() ,
,
所以 ![]() +(2n﹣1)2n﹣1 ①
+(2n﹣1)2n﹣1 ①
①×2得 ![]() +(2n﹣3)2n﹣1+(2n﹣1)2n ②
+(2n﹣3)2n﹣1+(2n﹣1)2n ②
①﹣②得: ![]() ﹣(2n﹣1)2n
﹣(2n﹣1)2n
= ![]() =1+2n+1﹣4﹣(2n﹣1)2n=﹣3﹣(2n﹣3)2n.
=1+2n+1﹣4﹣(2n﹣1)2n=﹣3﹣(2n﹣3)2n.
∴数列{cn}的前n项和 ![]() .
.
【解析】(1)由 ![]() 可求数列{an}的通项公式,进而可求数列{bn}通项公式;(2)由(1)可知
可求数列{an}的通项公式,进而可求数列{bn}通项公式;(2)由(1)可知 ![]() ,故可用错位相减法来求数列的前n项和.
,故可用错位相减法来求数列的前n项和.
【考点精析】本题主要考查了等差数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系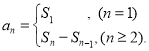 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】正项数列{an}的前n项和Sn满足:Sn2﹣(n2+n﹣1)Sn﹣(n2+n)=0
(1)求数列{an}的通项公式an;
(2)令bn= ![]() ,求数列{bn}的前n项和Tn , 证明:对于任意的n∈N* , 都有Tn
,求数列{bn}的前n项和Tn , 证明:对于任意的n∈N* , 都有Tn ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南通扬州泰州苏北四市高三二模】(本小题满分14分)
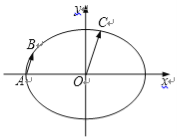
如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,C为椭
,C为椭
圆上位于第一象限内的一点.
(1)若点![]() 的坐标为
的坐标为![]() ,求a,b的值;
,求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且![]() ,求直线AB的斜率.
,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
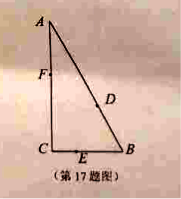
【题目】【2017镇江一模】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,
,
斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,所在位
大道上嬉戏,所在位
置分别记为点![]() .
.
(1)若甲乙都以每分钟![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,到大道的另一端
出发在各自的大道上奔走,到大道的另一端
时即停,乙比甲迟![]() 分钟出发,当乙出发
分钟出发,当乙出发![]() 分钟后,求此时甲乙两人之间的距离;
分钟后,求此时甲乙两人之间的距离;
(2)设![]() ,乙丙之间的距离是甲乙之间距离的
,乙丙之间的距离是甲乙之间距离的![]() 倍,且
倍,且![]() ,请将甲
,请将甲
乙之间的距离![]() 表示为
表示为![]() 的函数,并求甲乙之间的最小距离.
的函数,并求甲乙之间的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大,对某月即将出售的空调和冰箱进行了相关调查,得出下表:
资金 | 每台空调或冰箱所需资金(百元) | 月资金最多供应量(百元) | |
空调 | 冰箱 | ||
进货成本 | 30 | 20 | 300 |
工人工资 | 5 | 10 | 110 |
每台利润 | 6 | 8 | |
问:该商场如果根据调查得来的数据,应该怎样确定空调和冰箱的月供应量,才能使商场获得的总利润最大?总利润的最大值为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】100辆汽车通过某一段公路时,时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约有( )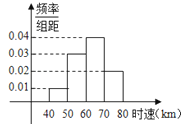
A.60辆
B.80辆
C.70辆
D.140辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面坐标系内,O为坐标原点,向量 ![]() =(1,7),
=(1,7), ![]() =(5,1),
=(5,1), ![]() =(2,1),点M为直线OP上的一个动点.
=(2,1),点M为直线OP上的一个动点.
(1)当 ![]()
![]() 取最小值时,求向量
取最小值时,求向量 ![]() 的坐标;
的坐标;
(2)在点M满足(I)的条件下,求∠AMB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com