
【题目】某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( ) 
A.
B.
C.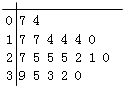
D.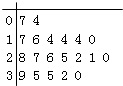
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是矩形,
是矩形, ![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

(1)当![]() 为何值时,
为何值时, ![]() 平面
平面![]() ?证明你的结论;
?证明你的结论;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系:  .(注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品).已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
.(注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品).已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量x为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,异面直线
,异面直线![]() 和
和![]() 所成角等于
所成角等于![]() .
.
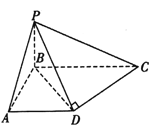
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ?若存在,指出点
?若存在,指出点![]() 在棱
在棱![]() 上的位置,若不存在,说明理由.
上的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)若从这![]() 天中随机抽取两天,求至少有
天中随机抽取两天,求至少有![]() 天参加抽奖人数超过
天参加抽奖人数超过![]() 的概率;
的概率;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续
,并估计若该活动持续![]() 天,共有多少名顾客参加抽奖.
天,共有多少名顾客参加抽奖.
参考公式:  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 
(1)求f(x)> ![]() 在x∈[0,π]上的解集;
在x∈[0,π]上的解集;
(2)设g(x)=2 ![]() cos2x+f(x),g(α)=
cos2x+f(x),g(α)= ![]() +
+ ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求sin2α的值.
),求sin2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该分店此次抽奖活动自开业始,持续![]() 天,参加抽奖的每位顾客抽到一等奖(价值
天,参加抽奖的每位顾客抽到一等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到二等奖(价值
,抽到二等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到三等奖(价值
,抽到三等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() .
.
试估计该分店在此次抽奖活动结束时送出多少元奖品?
参考公式: 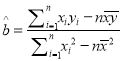 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程是
的参数方程是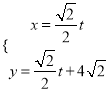 (
(![]() 是参数),以坐标原点为原点,
是参数),以坐标原点为原点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)过直线![]() 上的点作曲线
上的点作曲线![]() 的切线,求切线长的最小值.
的切线,求切线长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com