
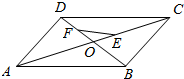
 已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )
已知平行四边形ABCD的对角线分别为AC,BD,且$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,则( )| A. | $\overrightarrow{FE}$=-$\frac{1}{12}$$\overrightarrow{AB}$-$\frac{5}{12}$$\overrightarrow{AD}$ | B. | $\overrightarrow{FE}$=$\frac{1}{12}$$\overrightarrow{AB}$-$\frac{5}{12}$$\overrightarrow{AD}$ | C. | $\overrightarrow{FE}$=$\frac{5}{12}$$\overrightarrow{AB}$-$\frac{1}{12}$$\overrightarrow{AD}$ | D. | $\overrightarrow{FE}$=-$\frac{5}{12}$$\overrightarrow{AB}$-$\frac{1}{12}$$\overrightarrow{AD}$ |
分析 $\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,可得$\overrightarrow{FO}$=$\frac{1}{4}\overrightarrow{DB}$,$\overrightarrow{OE}$=$\frac{1}{6}\overrightarrow{AC}$,$\overrightarrow{FE}$=$\overrightarrow{FO}+\overrightarrow{OE}$=$\frac{1}{4}\overrightarrow{DB}$+$\frac{1}{6}\overrightarrow{AC}$,又$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$,$\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow{BD}$,代入化简即可得出.
解答 解:∵$\overrightarrow{AE}$=2$\overrightarrow{EC}$,点F是BD上靠近D的四等分点,
∴$\overrightarrow{FO}$=$\frac{1}{4}\overrightarrow{DB}$,$\overrightarrow{OE}$=$\frac{1}{6}\overrightarrow{AC}$,
∴$\overrightarrow{FE}$=$\overrightarrow{FO}+\overrightarrow{OE}$=$\frac{1}{4}\overrightarrow{DB}$+$\frac{1}{6}\overrightarrow{AC}$,
∵$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$,$\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow{BD}$,
∴$\overrightarrow{FE}$=$\frac{1}{4}(\overrightarrow{AB}-\overrightarrow{AD})$+$\frac{1}{6}(\overrightarrow{AB}+\overrightarrow{AD})$
=$\frac{5}{12}\overrightarrow{AB}$-$\frac{1}{12}\overrightarrow{AD}$.
故选:C.
点评 本题考查了向量共线定理、向量的三角形法则,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
 已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.
已知某个几何体的三视图 (单位:cm) 如图所示,则这个几何体的体积为$3\sqrt{3}$cm2,它的表面积是$18+2\sqrt{3}$cm3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,(-1≤x≤1)}\\{x-1,(x≥1)}\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,(-1≤x≤1)}\\{x-1,(x≥1)}\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{6}$ | B. | $-\frac{6}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
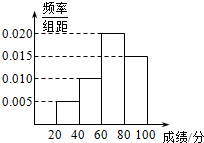 学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100),若低于60分的人数是15人,则该班的学生人数和平均成绩分别是( )
学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100),若低于60分的人数是15人,则该班的学生人数和平均成绩分别是( )| A. | 45,67 | B. | 50,68 | C. | 55,69 | D. | 60,70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com