练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

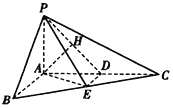
    【题目】在三棱锥中，平面，，，，是的中点，是线段上的一点，且.

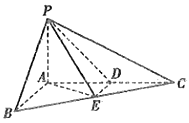
    （1）求证：平面；

    （2）求点到平面的距离.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）由已知易得是的中点，由平行平面内直线，证得平面；

    （2）设点到平面的距离为，利用，求得。

    （1）证明：因为，，，

    所以.

    因为，所以是的斜边上的中线，

    所以是的中点.

    又因为是的中点，所以.

    因为平面，平面，

    所以平面.

    （2）解法一：由（1）得，

    .

    .

    因为，所以.

    因为平面，所以.

    又，，所以平面.

    因为平面，所以.由（1）知，所以.

    在中，，

    所以.

    设点到平面的距离为，

    则由，得，即.

    解得.即点到平面的距离为.

    解法二：因为是的中点，

    所以点到平面的距离等于点到平面的距离.

    因为平面，所以.

    又，，所以平面.

    由（1）知，所以平面.又平面，

    所以平面平面.

    过作，垂足为，则平面，

    所以的长即为点到平面的距离.

    在中，由得.

    所以点到平面的距离为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某企业新研发了一种产品，产品的成本由原料成本及非原料成本组成.每件产品的非原料成本（元）与生产该产品的数量（千件）有关，经统计得到如下数据：

    1

    2

    3

    4

    5

    6

    7

    8

    112

    61

    44.5

    35

    30.5

    28

    25

    24

    根据以上数据，绘制了散点图.

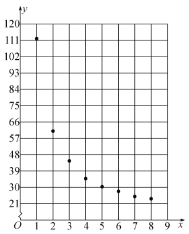
    观察散点图，两个变量不具有线性相关关系，现考虑用反比例函数模型和指数函数模型分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为，与的相关系数.

    参考数据（其中）：

    183.4

    0.34

    0.115

    1.53

    360

    22385.5

    61.4

    0.135

    （1）用反比例函数模型求关于的回归方程；

    （2）用相关系数判断上述两个模型哪一个拟合效果更好（精确到0.01），并用其估计产量为10千件时每件产品的非原料成本；

    （3）该企业采取订单生产模式（根据订单数量进行生产，即产品全部售出）.根据市场调研数据，若该产品单价定为100元，则签订9千件订单的概率为0.8，签订10千件订单的概率为0.2；若单价定为90元，则签订10千件订单的概率为0.3，签订11千件订单的概率为0.7.已知每件产品的原料成本为10元，根据（2）的结果，企业要想获得更高利润，产品单价应选择100元还是90元，请说明理由.

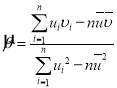    参考公式：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘估计分别为：，，相关系数.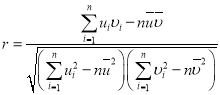

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动圆过定点且在轴上截得的弦长为4。

    （1）求动圆的圆心的轨迹的方程；

    （2）过点的动直线与曲线交于两点，点在曲线上，使得的重心在轴上，直线交轴于点，且点在点的右侧，记的面积为的面积为，求的最小值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数有两个不同的极值点，．

    （1）求的取值范围；

    （2）证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求曲线在处的切线方程；

    （2）函数在区间上有零点，求的值；

    （3）记函数，设是函数的两个极值点，若，且恒成立，求实数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018 年1月16日，由新华网和中国财经领袖联盟联合主办的2017中国财经年度人物评选结果揭晓，某知名网站财经频道为了解公众对这些年度人物是否了解，利用网络平台进行了调查，并从参与调查者中随机选出人，把这人分为 两类（类表示对这些年度人物比较了解，类表示对这些年度人物不太了解），并制成如下表格：

    年龄段

    岁～岁

    岁～岁

    岁～岁

    岁～岁

    人数

    类所占比例

    （1）若按照年龄段进行分层抽样，从这人中选出人进行访谈，并从这人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在岁～岁之间，另一名幸运者的年龄在岁～岁之间的概率；(注：从人中随机选出人,共有种不同选法)

    （2）如果把年龄在 岁～岁之间的人称为青少年，年龄在岁～岁之间的人称为中老年，则能否在犯错误的概率不超过的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异？

    参考数据：

    ，其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知过椭圆的左焦点，作斜率为的直线，交椭圆于两点.

    （1）若原点到直线的距离为，求直线的方程；

    （2）设点，直线与椭圆交于另一点，直线与椭圆交于另一点.设的斜率为，则是否为定值?若是，求出该定值；若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的焦距为，椭圆上任意一点到椭圆两个焦点的距离之和为6．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设直线 与椭圆交于两点，点（0，1），且=，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

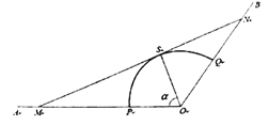
    【题目】如图，射线和均为笔直的公路，扇形区域（含边界）是一蔬菜种植园，其中、分别在射线和上.经测量得，扇形的圆心角（即）为、半径为1千米.为了方便菜农经营，打算在扇形区域外修建一条公路，分别与射线、交于、两点，并要求与扇形弧相切于点.设（单位：弧度），假设所有公路的宽度均忽略不计.

    （1）试将公路的长度表示为的函数，并写出的取值范围；

    （2）试确定的值，使得公路的长度最小，并求出其最小值.

    查看答案和解析>>

    同步练习册答案