
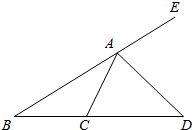
 如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?
如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗? 分析 分别在△ACD、△ABD中根据正弦定理列式,再将所得的式子相除并利用比例的性质,可得$\frac{AB}{AC}$=$\frac{BD}{DC}$成立.
解答 解:AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立理由如下: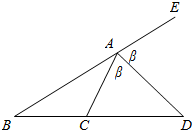
设∠CAD=∠DAE=β,
在△ACD中,由正弦定理得$\frac{DC}{sinβ}$=$\frac{AC}{sin∠D}$…①,
在△ABD中,由正弦定理得$\frac{BD}{sin∠BAD}$=$\frac{AB}{sin∠D}$,即$\frac{BD}{sin∠β}$=$\frac{AB}{sin∠D}$,…②,
②÷①可得 $\frac{AB}{AC}$=$\frac{BD}{DC}$,
结论成立
点评 本题考查了利用正弦定理解三角形等知识,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (1,3) | C. | (2,4) | D. | (3,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com