练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若a＜1，则关于的不等式x2-（a+1）x+a＜0的解集为
    {x|a＜x＜1}
    {x|a＜x＜1}
    ．
    分析：先将不等式x2-（a+1）x+a＜0因式分解，然后根据一元二次不等式的解法可求出所求．
    解答：解：∵x2-（a+1）x+a＜0
    ∴（x-1）（x-a）＜0
    ∵a＜1
    ∴a＜x＜1即不等式x2-（a+1）x+a＜0的解集为{x|a＜x＜1}
    点评：本题主要考查了一元二次不等式的解法，以及因式分解，同时考查了运算求解的能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下面关于向量的结论中，
    （1）|
    AB
    |=|
    BA
    |；
    （2）
    AB
    +
    BC
    +
    CD
    +
    DA
    =
    0
    ；
    （3）若
    a
    •
    b
    =0    ，则
    a
    ⊥
    b
    ；
    （4）若向量
    AB
    平移后，起点和终点的发生变化，所以
    AB
    也发生变化；
    （5）已知A、B、C、D四点满足任三点不共线，但四点共面，O是平面ABCD外任一点，且
    OA
    =2x•
    OB
    +3y•
    OC
    +4z•
    OD
    ，则2x+3y+4z=1．
    其中正确的序号为
    （1）（2）（3）（5）
    （1）（2）（3）（5）
    ．

    查看答案和解析>>

    科目：高中数学 来源：最新名师点评测试卷 高一数学 第一册上 题型：013

    下列结论中，不正确的是

    [　　]

    A．若a＞1，则与在定义域内均是增函数

    B．函数与的图象关于直线y＝x对称

    C．函数与y=2·表示同一个函数

    D．若0＜a＜1，0＜m＜n＜1，则一定有

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    下列结论中，不正确的是

    [　　]

    A．若a＞1，则与在定义域内均是增函数

    B．函数与的图象关于直线y＝x对称

    C．函数与y=2·表示同一个函数

    D．若0＜a＜1，0＜m＜n＜1，则一定有

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山东省青州市高三2月月考理科数学 题型：填空题

    给出下列六个命题：

    ①函数f（x）＝lnx－2＋x在区间（1 , e）上存在零点；

    ②若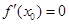，则函数y＝f（x）在x＝x0处取得极值；

    ③若m≥－1，则函数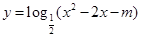的值域为R；

    ④“a=1”是“函数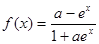在定义域上是奇函数”的充分不必要条件。

    ⑤函数y=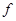（1+x）的图像与函数y=f（l-x）的图像关于y轴对称；        

      ⑥满足条件AC=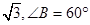，AB =1的三角形△ABC有两个．

    其中正确命题的个数是      　   。

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列五个命题：

    ①函数f（x）＝lnx－2＋x在区间（1 , e）上存在零点；

    ②若，则函数y＝f（x）在x＝x0处取得极值；

    ③若m≥－1，则函数的值域为R；

    ④“a=1”是“函数在定义域上是奇函数”的充分不必要条件。

    ⑤函数y=（1+x）的图像与函数y=f（l-x）的图像关于y轴对称；          

    其中正确命题的序号是_____________（请填上所有正确命题的序号）

    查看答案和解析>>

    同步练习册答案