
【题目】已知![]() .
.
(I)讨论![]() 的单调性;
的单调性;
(II)当![]() 有最大值,且最大值大于
有最大值,且最大值大于![]() 时,求a的取值范围.
时,求a的取值范围.
【答案】
(1)见解析(2)(0,1).
【解析】
试题分析:
(1)由题已知函数的解析式(注意定义域),可运用导数求出函数的单调区间。即:![]() 为函数的增区间,反之为减区间。由导函数中含有字母参数,需分类讨论;
为函数的增区间,反之为减区间。由导函数中含有字母参数,需分类讨论;
(2)由题给出了函数的最大值的范围大于![]() ,再结合(1)已知函数的单调区间,可对应单调性,表示出函数的最大值,从而建立不等式lna+a-1<0,需构造函数利用单调性解出不等式的解,而求出
,再结合(1)已知函数的单调区间,可对应单调性,表示出函数的最大值,从而建立不等式lna+a-1<0,需构造函数利用单调性解出不等式的解,而求出![]() 的取值范围。
的取值范围。
试题解析:
(Ⅰ)f(x)=lnx+a(1﹣x)的定义域为(0,+∞),∴f′(x)=![]() ﹣a=
﹣a=![]() ,
,
若a≤0,则f′(x)>0,∴函数f(x)在(0,+∞)上单调递增,
若a>0,则当x∈(0,![]() )时,f′(x)>0,
)时,f′(x)>0,
当x∈(![]() ,+∞)时,f′(x)<0,所以f(x)在(0,
,+∞)时,f′(x)<0,所以f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减,
,+∞)上单调递减,
(Ⅱ)由(Ⅰ)知,当a≤0时,f(x)在(0,+∞)上无最大值;
当a>0时,f(x)在x=![]() 取得最大值,最大值为f(
取得最大值,最大值为f(![]() )=﹣lna+a-1,
)=﹣lna+a-1,
∵f(![]() )>2a﹣2,∴lna+a-1<0,
)>2a﹣2,∴lna+a-1<0,
令g(a)=lna+a-1,∵g(a)在(0,+∞)单调递增,g(1)=0,
∴当0<a<1时,g(a)<0,当a>1时,g(a)>0,∴a的取值范围为(0,1).


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】某公益基金收到甲乙丙三人的20万、25万、30万三笔捐款(一人捐一笔款),记者采访这三兄弟时,甲说:“乙捐的不是最少.”乙说:“甲捐的比丙多.”丙说:“若我捐的最少,则甲捐的不是最多.”根据这三人的回答,确定乙捐了_________万.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机![]() 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为![]() 万元,且
万元,且
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万只)的函数解析式;
(万只)的函数解析式;
(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从![]() 地到
地到![]() 地共有两条路径
地共有两条路径![]() 和
和![]() ,据统计,经过两条路径所用的时间互不影响,且经过
,据统计,经过两条路径所用的时间互不影响,且经过![]() 和
和![]() 所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。
所用时间落在各时间段内的频率分布直方图分别为下图(1)和(2)。

现甲、乙两人分别有40分钟和50分钟时间用于从![]() 地到
地到![]() 地。
地。
(1)为了尽最大可能在各自允许的时间内赶到![]() 地,甲和乙应如何选择各自的路径?
地,甲和乙应如何选择各自的路径?
(2)用![]() 表示甲、乙两人中在允许的时间内能赶到
表示甲、乙两人中在允许的时间内能赶到![]() 地的人数,针对(1)的选择方案,求
地的人数,针对(1)的选择方案,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
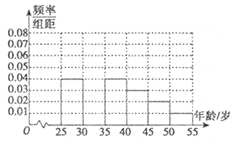
【题目】近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否喜欢骑车锻炼”的问卷,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否喜欢骑车锻炼”的问卷,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如下统计表和各年龄段人数频率分布直方图:

(1)补全频率分布直方图,并![]() 的值;
的值;
(2)从![]() 岁年龄段的“喜欢骑车”中采用分层抽样法抽取6人参加骑车锻炼体验活动,求其中选取2名领队来自同一组的概率。
岁年龄段的“喜欢骑车”中采用分层抽样法抽取6人参加骑车锻炼体验活动,求其中选取2名领队来自同一组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以![]() 表示和为6的事件,求
表示和为6的事件,求![]() ;
;
(2)现连玩三次,若以![]() 表示甲至少赢一次的事件,
表示甲至少赢一次的事件,![]() 表示乙至少赢两次的事件,试问
表示乙至少赢两次的事件,试问![]() 与
与![]() 是否为互斥事件?为什么?
是否为互斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com