已知f(x)定义域为R,满足:
①f(1)=1>f(-1);
②对任意实数x,y,有f(y-x+1)=f(x)f(y)+f(x-1)f(y-1).
(Ⅰ)求f(0),f(3)的值;
(Ⅱ)判断函数的奇偶性与周期性,并求f2(3x)+f2(3x-1)的值;
(Ⅲ)是否存在常数A,B,使得不等式|f(x)+f(2-x)+Ax+B|≤2对一切实数x成立.如果存在,求出常数A,B的值;如果不存在,请说明理由.
解:(Ⅰ)∵f(y-x+1)=f(x)f(y)+f(x-1)f(y-1),
∴令x=y=1,得f(1-1+1)=f(1)f(1)+f(0)f(0),
即f(1)=f2(1)+f2(0),
∵f(1)=1,∴f(0)=0,
令x=y=0得,f(1)=f2(0)+f2(-1),
∵f(1)=1>f(-1),∴f(-1)=-1,
令x=0、y=2得,f(3)=f(0)f(2)+f(-1)f(1),
∴f(3)=-f(1)=-1,
(Ⅱ)对f(y-x+1)=f(x)f(y)+f(x-1)f(y-1),
令y=0,得f(-x+1)=f(x)f(0)+f(x-1)f(-1)
由(1)得,f(-1)=-1,f(0)=0,
∴f(-x+1)=-f(x-1),令x=x+1,即f(-x)=-f(x),
∴函数为奇函数,
令x=-x-1,代入f(-x+1)=-f(x-1),
得f(-x+2)=-f(-x)=f(x),即f(2-x)=f(x),
∴-f(x-2)=f(x),令x=x+2代入得f(x+2)=-f(x),
令x=x+2代入得f(x+4)=f(x),
∴函数的周期是4,
令x=y代入f(y-x+1)=f(x)f(y)+f(x-1)f(y-1),
得f2(x)+f2(x-1)=1,令x=3x代入得,
∴f2(3x)+f2(3x-1)=1,
(Ⅲ)假设存在常数A,B满足题意,
由(II)得,f(2-x)=f(x),
∴|f(x)+f(2-x)+Ax+B|≤2为:|2f(x)+Ax+B|≤2,
令x=-1得,-2≤-2-A+B≤2,即-2≤2+A-B≤2 ①
令x=1得,-2≤2+A+B≤2 ②
令x=3得,-2≤-2+3A+B≤2,即-2≤2-3A-B≤2 ③
①+②得,-4≤A≤0;②+③得,0≤A≤4,则A=0,
将A=0代入①得0≤B≤4;代入②得-4≤B≤0,则B=0,
由(II)得,f2(x)+f2(x-1)=1,
∴当A=B=0时,|2f(x)+Ax+B|≤2对一切实数x成立,
∴存在唯一一组常数A=B=0,使得不等式|f(x)+f(2-x)+Ax+B|≤2对一切实数x成立.
分析:(I)令x=y=1代入式子,得f(1)=f2(1)+f2(0),由f(1)=1得f(0)=0,
再令x=y=0代入式子化简后,根据f(1)=1>0>f(-1),得f(-1)=-1,令x=0、y=2求出f(3)的值;
(II)令y=0得f(-x+1)=f(x)f(0)+f(x-1)f(-1),再根据(1)得f(-x+1)=-f(x-1),即f(-x)=-f(x),判断出函数为奇函数,令x=-x-1,代入f(-x+1)=-f(x-1)进行化简,结合奇函数的性质求出函数的周期,令x=y代入f(y-x+1)=f(x)f(y)+f(x-1)f(y-1),求出f2(x)+f2(x-1)=1,令x=3x代入求出f2(3x)+f2(3x-1)的值;
(Ⅲ)假设存在常数A,B满足题意,根据(II):f(2-x)=f(x),将不等式转化为:|2f(x)+Ax+B|≤2,分别x=-1、1、3列出方程,再相加后求出A和B的值,再根据f2(x)+f2(x-1)=1进行判断即可.
点评:本题考查了函数奇偶性的判断,和抽象函数的性质和求值的问题,以及存在性问题,属于难题.合理地利用条件赋值,是解决本题的关键所在.



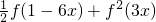 的值;
的值;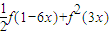 的值;
的值;