
【题目】已知函数 ![]() ,g(x)=2ln(x+m).
,g(x)=2ln(x+m).
(1)当m=0,存在x0∈[ ![]() ,e](e为自然对数的底数),使
,e](e为自然对数的底数),使 ![]() ,求实数a的取值范围;
,求实数a的取值范围;
(2)当a=m=1时,设H(x)=xf(x)+g(x),在H(x)的图象上是否存在不同的两点A(x1 , y1),B(x2 , y2)(x1>x2>﹣1),使得H(x1)﹣H(x2)= ![]() ?请说明理由.
?请说明理由.
【答案】
(1)解:x0f(x0)≥g(x0)可化为 ![]() ,
,
令h(x)=x2﹣2lnx,则 ![]()
∴当x∈ ![]() 时,h'(x)<0;当x∈(1,e]时,h'(x)>0;
时,h'(x)<0;当x∈(1,e]时,h'(x)>0;
又∵ ![]() ,∴
,∴ ![]() ,则a≤e2﹣2
,则a≤e2﹣2
(2)解:H(x)=x2+2ln(x+1)﹣1, ![]() ;
;
![]() ;
;
![]() ;
;
故可化为 ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
又即 ![]() =
= 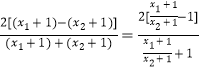 ①,
①,
令 ![]() ,①式可化为
,①式可化为 ![]() ,
,
令 ![]() ,
, ![]() ,∴u(t)在(1,+∞)上递增
,∴u(t)在(1,+∞)上递增
∴u(t)≥u(1)=0;∴u(t)无零点,故A、B两点不存在
【解析】(1)x0f(x0)≥g(x0)可化为 ![]() , 构造h(x)=x2﹣2lnx,求出其值域即可.(2)
, 构造h(x)=x2﹣2lnx,求出其值域即可.(2) ![]() ;
; ![]() ;
;
故可化为 ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
又即 ![]() =
= 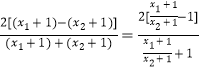 ①,
①,
令 ![]() ,①式可化为
,①式可化为 ![]()
令 ![]() ,
, ![]() ,只需考查u(t)的值域即可.
,只需考查u(t)的值域即可.
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x+1)= ![]() ,且f(x)是偶函数,当x∈[0,1]时,f(x)=x,若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是 .
,且f(x)是偶函数,当x∈[0,1]时,f(x)=x,若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数![]() 与雾霾天数
与雾霾天数![]() 进行统计分析,得出下表数据.
进行统计分析,得出下表数据.
| 4 | 5 | 7 | 8 |
| 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图,并说明其相关关系;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
(相关公式: ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断错误的是______(填写序号)
①集合{y|y=![]() }有4个子集;
}有4个子集;
②若α≠β,则tanα≠tanβ;
③若log2a>log2b,则2a>2b;
④设函数f(x)=log2x的反函数为g(x),则g(2)=1;
⑤已知定义在R上的奇函数f(x)在(-∞,0)内有1008个零点,则函数f(x)的零点个数为2017.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex+2x2-3x.
(1)求证:函数f (x)在区间[0,1]上存在唯一的极值点.
(2)当x≥![]() 时,若关于x的不等式f (x)≥
时,若关于x的不等式f (x)≥![]() x2+(a-3)x+1恒成立,试求实数a的取值范围.
x2+(a-3)x+1恒成立,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+![]() 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0,![]() ]上是减函数,在[
]上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知(x)=![]() ,x∈[0,1]利用上述性质,求函数f(x)的值域;
,x∈[0,1]利用上述性质,求函数f(x)的值域;
(2)对于(1)中的函数f(x)和函数g(x)=-x+2a.若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知长方形ABCD,AD=2CD=4,M、N分别为AD、BC的中点,将长方形ABCD沿MN折到MNFE位置,且使平面MNFE⊥平面ABCD.
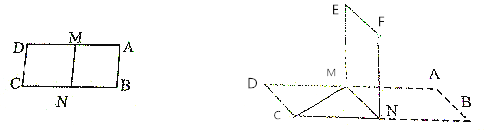
(1)求证:直线CM⊥面DFN;
(2)求点C到平面FDM的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com